2023年春季北师版数学九年级下册总复习检测B
试卷更新日期:2022-11-26 类型:期末考试
一、单选题(每题3分,共30分)
-
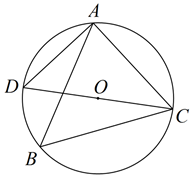
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 如图, 内接于 ,CD是 的直径, ,则 ( )
 A、70° B、60° C、50° D、40°3. 将抛物线y=x2向上平移3个单位,所得抛物线的解析式是( )A、y=x2+3 B、y=x2-3 C、y=(x+3)2 D、y=(x-3)24. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
A、70° B、60° C、50° D、40°3. 将抛物线y=x2向上平移3个单位,所得抛物线的解析式是( )A、y=x2+3 B、y=x2-3 C、y=(x+3)2 D、y=(x-3)24. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )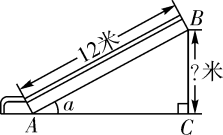 A、 米 B、 米 C、 米 D、 米5. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )
A、 米 B、 米 C、 米 D、 米5. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )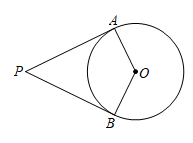 A、 B、 C、 D、6. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或47. 如图,是的高,若 , , 则边的长为( )
A、 B、 C、 D、6. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或47. 如图,是的高,若 , , 则边的长为( ) A、 B、 C、 D、8. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
A、 B、 C、 D、8. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )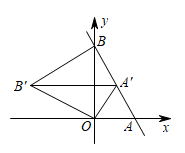 A、 B、 C、2 D、9. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、2 D、9. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )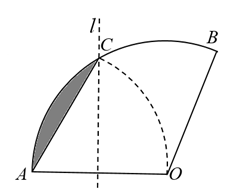 A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )
A、 B、 C、 D、10. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )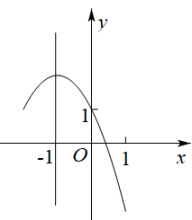 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(每空3分,共18分)
-
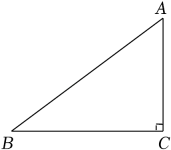
11. 如图,在Rt△ABC中,∠C=90°,若sinA= , 则cosB= .
 12. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
12. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )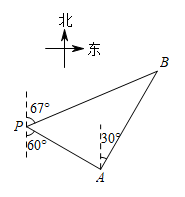 13. 如图,在⊙O内接四边形 中,若 ,则 .
13. 如图,在⊙O内接四边形 中,若 ,则 .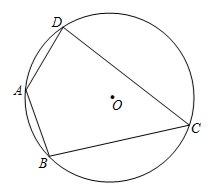 14. 已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 .
14. 已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 . 15. 如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是(结果保留)
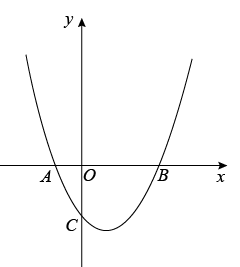
15. 如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧的长是(结果保留)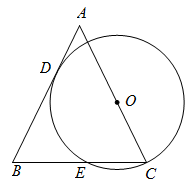 16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
三、解答题(共0题,共72分)
-
17. 计算:2sin60°﹣|﹣2|+(π﹣)0﹣+(﹣)﹣2.18. 计算:tan30°+|1﹣ |+(π﹣ )0﹣( )﹣1+ .19. 为了进一步改善人居环境,提高居民生活的幸福指数.某小区物业公司决定对小区环境进行优化改造.如图,AB表示该小区一段长为的斜坡,坡角于点D.为方便通行,在不改变斜坡高度的情况下,把坡角降为.
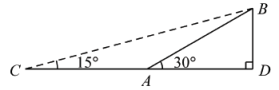 (1)、求该斜坡的高度BD;(2)、求斜坡新起点C与原起点A之间的距离.(假设图中C,A,D三点共线)20. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
(1)、求该斜坡的高度BD;(2)、求斜坡新起点C与原起点A之间的距离.(假设图中C,A,D三点共线)20. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题: (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).21. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).21. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.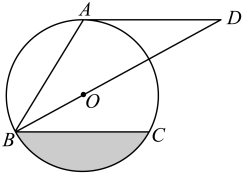 (1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.22. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.22. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.∵ ,
∴ ,
∴
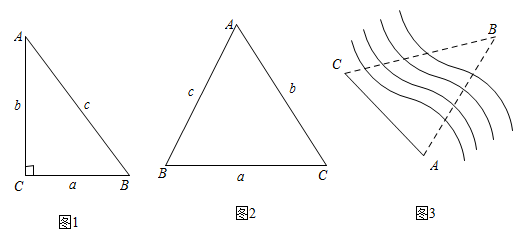 (1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.23. 如图,二次函数的图象与y轴相交于点A,与反比例函数的图象相交于点B(3,1).
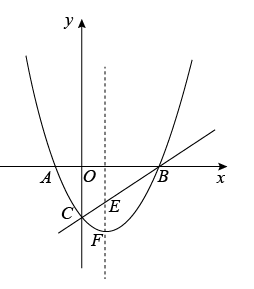
(1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.23. 如图,二次函数的图象与y轴相交于点A,与反比例函数的图象相交于点B(3,1).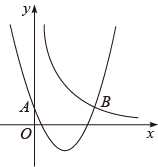 (1)、求这两个函数的表达式;(2)、当随x的增大而增大且时,直接写出x的取值范围;(3)、平行于x轴的直线l与函数的图象相交于点C、D(点C在点D的左边),与函数的图象相交于点E.若△ACE与△BDE的面积相等,求点E的坐标.
(1)、求这两个函数的表达式;(2)、当随x的增大而增大且时,直接写出x的取值范围;(3)、平行于x轴的直线l与函数的图象相交于点C、D(点C在点D的左边),与函数的图象相交于点E.若△ACE与△BDE的面积相等,求点E的坐标.