浙教版备考2023年中考数学一轮复习23.分式方程及其应用

试卷更新日期：2022-11-26 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列关于 $x$ 的方程： $\frac{1}{x} + x = 1 ， \frac{x}{3} + \frac{3 x}{4} = \frac{2}{5} ， \frac{1}{x - 1}$ $= \frac{4}{x} ， \frac{x^{2} - 1}{x + 1} = 2$ 中，分式方程的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 已知关于x的方程 $\frac{3}{x}$ = $\frac{k}{3 - x}$ 的解是正整数，且k为整数，则k的值是（）

A、0 B、-2 C、0或6 D、-2或6

查看试题解析
3. 若关于x的方程 $\frac{2 x}{x - 3} - 1 = \frac{m - 1}{3 - x}$ 无解，则m的值为（）

A、﹣5 B、7 C、5 D、﹣3

查看试题解析
4. 要把分式方程 $\frac{3}{2 x - 4} = \frac{1}{x}$ 化为整式方程，方程两边要同时乘以（）

A、 $2 x - 4$ B、 $x$ C、 $2 (x - 2)$ D、 $2 x (x - 2)$

查看试题解析
5. 用换元法解分式方程 $\frac{x + 1}{x} + \frac{6 x}{x + 1} = 5$ ，如果设 $\frac{x + 1}{x} = y$ ，将原方程化为关于y的整式方程，那么这个整式方程是（）

A、 $y + \frac{6}{y} = 5$ B、 $y^{2} + 5 y + 6 = 0$ C、 $y^{2} - 5 y + 6 = 0$ D、 $y^{2} + 6 y - 5 = 0$

查看试题解析
6. 如果关于x的分式方程 $\frac{x - a}{x - 2}$ ＝1+ $\frac{5 - 2 x}{x - 2}$ 有正整数解，且关于y的一元一次不等式组 ${\begin{cases} \frac{3 y - 3}{4} > y - 2 \\ y - a \leq 0 \end{cases}$ 的解集为y≤a，则所有满足条件的整数a的和为（）

A、8 B、7 C、3 D、2

查看试题解析
7. 下列说法：① $\frac{5 x + 1}{3 x}$ = $\frac{2}{x}$ 是分式方程；②x=1或x=﹣1是分式方程 $\frac{x + 1}{x^{2} - 1}$ =0的解；③分式方程 $\frac{3}{x + 4}$ = $\frac{2}{x}$ 转化成一元一次方程时，方程两边需要同乘x（x+4）；④解分式方程时一定会出现增根，其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 甲、乙两人分别从A、B两地同时出发，骑自行车前往C地．已知A，C两地相距 $60 k m$ ， B，C两地相距 $50 k m$ ，甲骑行的平均速度比乙骑行的平均速度快 $3 k m / h$ ，两人同时到达C地．设乙骑行的平均速度为 $x k m / h$ ，则所列方程正确的是（）

A、 $\frac{60}{x} = \frac{50}{x + 3}$ B、 $\frac{60}{x + 3} = \frac{50}{x}$ C、 $\frac{60}{x - 3} = \frac{50}{x}$ D、 $\frac{60}{x} = \frac{50}{x - 3}$

查看试题解析
9. 某工程队承接了60万平方米的绿化工程，由于情况有变， $\dots .$ 设原计划每天绿化的面积为 $x$ 万平方米，列方程为 $\frac{60}{(1 - 20 %) x} - \frac{60}{x} = 30$ ，根据方程可知省略的部分是（）

A、实际工作时每天的工作效率比原计划提高了20%，结果提前30天完成了这一任务 B、实际工作时每天的工作效率比原计划提高了20%，结果延误30天完成了这一任务 C、实际工作时每天的工作效率比原计划降低了20%，结果延误30天完成了这一任务 D、实际工作时每天的工作效率比原计划降低了20%，结果提前30天完成了这一任务

查看试题解析
10. 某物美超市同时卖出了两个进价不同的冰墩墩 $A$ 和 $B$ ，售价均为90元，按成本计算，超市人员发现冰墩墩 $A$ 盈利了50%，而冰墩墩 $B$ 却亏损了40%，则这次超市是（）

A、不赚不赔 B、赚了 C、赔了 D、无法判断

查看试题解析

二、填空题（每题4分，共24分）

11. 写出一个解为1的分式方程：．

查看试题解析
12. 若方程 $\frac{2}{1 - x} = \frac{x}{x - 1} - 3$ 的解为 $x = \frac{5}{2}$ ，则方程 $\frac{2}{1 - 2 y} = \frac{2 y}{2 y - 1} - 3$ 的解为 $y =$ ．

查看试题解析
13. 若分式 $\frac{2}{x - 3}$ 的值为2，则 $x$ 的值为.

查看试题解析
14. 已知方程 $\frac{x^{2} + 1}{x} - \frac{x}{x^{2} + 1} = 3$ ，如果设 $\frac{x}{x^{2} + 1} = y$ ，那么原方程可以变形为．

查看试题解析
15. 甲、乙两人在社区进行核酸采样，甲每小时比乙每小时多采样10人，甲采样160人所用时间与乙采样140人所用时间相等，甲、乙两人每小时分别采样多少人？设甲每小时采样x人，则可列分式方程为．

查看试题解析
16. 对于实数a、b，定义一种新运算“※”为： $a ※ b = \frac{1}{a - b^{2}}$ ，例如： $1 ※ 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x ※ (- 3) = \frac{2}{9 - x} - 1$ 的解是．

查看试题解析

三、解答题（共8题，共66分）

17. 解方程： $1 - \frac{1}{x^{2} + 7 x + 6} = \frac{x^{2} - 5 x + 5}{x^{2} - 5 x + 6}$

查看试题解析
18. 如果方程 $\frac{2 x - 3}{5} = \frac{2}{3} x - 2$ 与 $3 a - \frac{1}{4} = 3 (x + a) - 2 a$ 的解相同，求（a-3）²的值.

查看试题解析
19. 在实数范围内只有一个实数是关于x的方程 $\frac{k (x - 1)}{x} + \frac{2 k + 1}{x^{2} + x} = 1 + \frac{2 k}{x + 1}$ 的根，求实数k的所有可能值.

查看试题解析
20. 我们把形如 $x + \frac{a b}{x} = a + b (a ， b$ 不为零 $)$ ，且两个解分别为 $x_{1} = a$ ， $x_{2} = b$ 的方程称为“十字分式方程”.
例如 $x + \frac{3}{x} = 4$ 为十字分式方程，可化为 $x + \frac{1 \times 3}{x} = 1 + 3$ ， $∴ x_{1} = 1$ ， $x_{2} = 3$ .

再如 $x + \frac{8}{x} = - 6$ 为十字分式方程，可化为 $x + \frac{(- 2) \times (- 4)}{x} = (- 2) + (- 4)$ ， $∴ x_{1} = - 2$ ， $x_{2} = - 4$ .

应用上面的结论解答下列问题：

(1)、若 $x + \frac{6}{x} = - 5$ 为十字分式方程，则 $x_{1} =$ ， $x_{2} =$ .

(2)、若十字分式方程 $x - \frac{5}{x} = - 2$ 的两个解分别为 $x_{1} = m$ ， $x_{2} = n$ ，求 $\frac{n}{m} + \frac{m}{n}$ 的值.

(3)、若关于 $x$ 的十字分式方程 $x - \frac{2 k^{2} + 3 k}{x - 2} = - k - 1$ 的两个解分别为 $x_{1}$ ， $x_{2} (k > 0 ， x_{1} > x_{2})$ ，求 $\frac{x_{1} - 2}{x_{2} + 1}$ 的值.

查看试题解析
21. 在福州地铁6号线某段工程建设中，甲队单独完成这项工程需要150天，甲队单独施工30天后增加乙队，两队又共同工作了15天，共完成总工程的 $\frac{1}{3}$ .

(1)、求乙队单独完成这项工程需要多少天？

(2)、为了加快工程进度，甲、乙两队各自提高工作效率，提高后甲队的工作效率是乙队工作效率的 $m$ 倍，若两队合作40天完成剩余的工程，求乙队提高后的工作效率是提高前工作效率的几倍（用含 $m$ 的式子表示）.

查看试题解析
22. 化学实验室一容器内的a克盐水中含盐b克（盐水的浓度＝含盐质量÷盐水质量×100%）.

(1)、若加入4克盐，食盐水的浓度怎么变化，为什么？（用数学的方法书写过程）

(2)、若a＝50，b＝5，加多少克盐可使该容器内的盐水浓度提高到原来的2倍？

(3)、若a＝50，b＝5，则需要蒸发多少克水，使该容器内的盐水浓度提高到原来的2倍.

查看试题解析
23. 金师傅近期准备换车，看中了价格相同的两款国产车．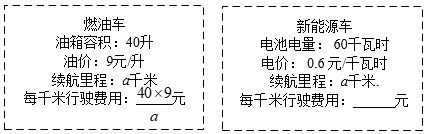

(1)、用含a的代数式表示新能源车的每千米行驶费用．

(2)、若燃油车的每千米行驶费用比新能源车多0.54元．
①分别求出这两款车的每千米行驶费用．

②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

查看试题解析
24. 猕猴桃被誉为“维C之王”，其中含血清促进素可以稳定情绪，丰富膳食纤维能促进心脏健康．在泰顺猕猴桃销售旺季时，爸爸妈妈让他们的两个孩子泰泰与顺顺去猕猴桃市场采购相同价格的同一种猕猴桃．泰泰用240元买的猕猴桃数量比顺顺用300元买的猕猴桃数量少10斤．

(1)、求这种猕猴桃的单价．

(2)、两人第二次再去采购该种猕猴桃时，每斤单价比上次少了2元．两个人购买方案不同如图所示．他们想通过这两次购买体验，作为数学项目化学习的一个素材，探究谁的购买方案更加合算．计算得泰泰两次购买的猕猴桃平均价格是元/斤，顺顺两次购买的猕猴桃平均价格是元/斤．

(3)、泰泰和顺顺通过这次购买弥猴桃的项目化学习，总结出连续购买某种商品更合算的方案，并迁移联想到爸爸的加油习惯是按照同样的金额加油，而妈妈总是说"把油箱加满"。他们要建议父母按相同的（填“金额”或“油量"）加油更合算．请你通过计算说明理由．

查看试题解析