浙教版备考2023年中考数学一轮复习22.一元二次方程的应用（1）

试卷更新日期：2022-11-26 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 九年级1907班文学小组在举行的图书共享仪式上互赠图书，每个同学都把自己的图书向本组其他成员赠送一本，全组共互赠了132本图书，如果设全组共有 $x$ 名同学，依题意，可列出的方程是（）

A、 $x (x + 1) = 132$ B、 $\frac{1}{2} x (x - 1) = 132$ C、 $2 x (x - 1) = 132$ D、 $x (x - 1) = 132$

查看试题解析
2. 某班组织了一次小型同学聚会，参与的同学每两人之间都握了一次手，所有人共握了45次手，设其有 $x$ 位同学会，则 $x$ 满足的关系式为（）

A、 $\frac{1}{2} x (x + 1) = 45$ B、 $\frac{1}{2} x (x - 1) = 45$ C、 $x (x + 1) = 45$ D、 $x (x - 1) = 45$

查看试题解析
3. 如图，在宽为 $20 m$ 、长为 $30 m$ 的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要 $504 m^{2}$ ，则修建的路宽应为（　　　）

A、 $1 m$ B、 $1.5 m$ C、 $2 m$ D、 $2.5 m$

查看试题解析
4. 某牧民要围成面积为35 $m^{2}$ 的矩形羊圈，且长比宽多2米，则此羊圈的周长是（）

A、20米 B、24 米 C、26 米 D、20或22米

查看试题解析
5. 李明去参加聚会，每两人都互相赠送礼物，他发现共送礼物30件，若设有n人参加聚会，根据题意可列出方程为（）

A、 $\frac{n (n + 1)}{2} = 30$ B、n（n﹣1）＝30 C、 $\frac{n (n - 1)}{2} =$ 30 D、n（n＋1）＝30

查看试题解析
6. 某广场有一块正方形的空地正中间修建一个圆形喷泉，在四个角修建四个四分之一圆形的水池，其余部分种植花草，若喷泉和水池的半径都相同，喷泉边缘到空地边界的距离为3m，种植花草的区域的面积为100m，设水池半径为xm，可列出方程（）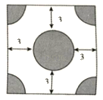

A、（2x+3）²﹣πx²＝100 B、（x+6）²﹣πx²＝100 C、（2x+3）²﹣2x²＝100 D、（2x+6）²﹣2πx²＝100

查看试题解析
7. 一种病毒每轮传播的人数为x．若某人被感染后，未经有效防护，经过两轮传播共感染了144人，则x为（）

A、11 B、12 C、13 D、14

查看试题解析
8. 欧几里得的《原本》记载，形如 $x^{2} + a x = b^{2}$ 的方程的图解法是：画 $R t Δ A B C$ ，使 $∠ A C B = 9 0^{∘}$ ， $B C = \frac{a}{2}$ ， $A C = b$ ，再在斜边 $A B$ 上截取 $B D = \frac{a}{2}$ .则该方程的一个正根是（）

A、 $A C$ 的长 B、 $A D$ 的长 C、 $B C$ 的长 D、 $C D$ 的长

查看试题解析
9. 某年级举行篮球比赛，每一支球队都和其他球队进行了一场比赛，已知共举行了21场比赛，那么共有（）支球队参加了比赛．

A、6 B、12 C、7 D、14

查看试题解析
10. 在肥西悬主城区，共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多690辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（）

A、 $1000 {(1 + x)}^{2} = 1000 + 690$ B、 $1000 {(1 + x)}^{2} = 690$ C、 $690 {(1 + x)}^{2} = 1000$ D、 $1000 (1 + 2 x) = 1000 + 690$

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 30 c m$ ， $B C = 21 c m$ ，动点 $P$ 从点 $C$ 出发，沿 $C A$ 方向运动，动点 $Q$ 从点 $B$ 出发，沿 $B C$ 方向运动，如果点 $P$ ， $Q$ 同时出发， $P$ ， $Q$ 的运动速度均为 $1 c m / s$ ．那么运动秒时，它们相距 $15 c m$ ．

查看试题解析
12. 如图是某停车场的平面示意图，停车场外围的长为30米，宽为18米．停车场内车道的宽都相等．停车位总占地面积为288平方米．设车道的宽为x米，可列方程为．

查看试题解析
13. 在小海的某个微信群中，若每人给其他成员都发一个红包，该微信群共发了90个红包，设这个微信群共有x个人，则可列出方程为。

查看试题解析
14. 2022年女足亚洲杯在2022年1月20日至2月6日举行，由小组赛和淘汰赛组成．按比赛规则小组赛赛制为单循环赛制（即每个小组的两个球队之间进行一场比赛），在小组赛阶段，中国队凭借着小组赛比赛前几个场次的赢球，成为最先获得八强资格的球队，并在2022年2月6日的亚洲杯决赛中以3∶2战胜韩国女足，获得亚洲杯冠军．已知中国女足队所在的A组共安排了6场比赛，则中国女足所在的A组共有支球队．

查看试题解析
15. 小明在计算某数的平方时，将这个数的平方误看成它的2倍，使答案少了35，则这个数为．

查看试题解析
16. 某种植物的主干长出若干数目的支干，每个支干又长出同样多数目的小分支，主干、支干、小分支一共是43个，则每个支干长出的小分支数目为．

查看试题解析

三、解答题（共8题，共66分）

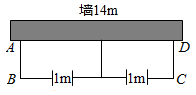
17. 某种肺炎病毒在A国爆发，经世卫组织研究发现：病毒有极强的传染性，一个病毒携带者与10个人有密切接触，其中的6人会感染病毒，成为新的病毒携带者.在调查某工厂的疫情时，发现最初只有1位出差回来的病毒携带者，在召开工厂车间组长会议时发生了第一轮传染，开完会后所有人都回到各自车间工作又发生了第二轮传染，这时全厂一共有169人检测出携带病毒.假如每个病毒携带者每次的密切接触者人数都相同，求每个病毒携带者每次的密切接触了多少人？

查看试题解析
18. 如图，用长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃ABCD，为了方便出入，在建造篱笆花圃时，在BC上用其他材料做了宽为1米的两扇小门．若花圃的面积刚好为45m² ，求花圃的长与宽．

查看试题解析
19. 我县某宾馆有若干间标准房，平时以市场管理部门批准的标价200元定价时（定价不得超过380元），平均每日可入住50间，在去年国庆黄金周中，为了增加营业额，该宾馆决定上调房价，经市场调查表明，定价每提高20元，每日入住房间数就减少1间，若不考虑其他因素，问国庆期间宾馆标准房的价格定为多少元时，每日的营业额可为11520元？

查看试题解析
20. 为了响应“践行核心价值观，传递青春正能量”的号召，小颖决定走入社区号召大家参加“传递正能量志愿服务者”.假定从一个人开始号召，每一个人每周能够号召相同的m个人参加，被号召参加的人下一周会继续号召，两周后，将有121人被号召成为“传递正能量志愿服务者”.

(1)、求出m的值；

(2)、经过计算后，小颖、小红、小丽三人开始发起号召，但刚刚开始，他们就发现了问题，实际号召过程中，不是每一次号召都可以成功，而他们三人的成功率也各不相同，已知小红的成功率比小颖的两倍少10%，第一周后小丽比小颖多号召2人，三人一共号召17人，其中小颖号召了n人.请分别求出他们三人号召的成功率.

查看试题解析
21. 某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在EH、FG、BC上各留1米宽的门（不用木栏），建成后木栏总长45米．

(1)、若饲养场（矩形ABCD）的一边CD长为7米，求BC＝米．

(2)、若饲养场（矩形ABCD）的面积为192平方米，求边CD的长．

(3)、饲养场的面积能达到198平方米吗？若能达到，求出边CD的长；若不能达到，请说明理由．

查看试题解析
22. 某花卉生产基地举行花卉展览，如图所示是用这两种花卉摆成的图案，白色圆点为盆景，灰色圆点为盆花．图1中盆景数量为2，盆花数量为2；图2中盆景数量为4，盆花数量为6；图3中盆景数量为6，盆花数量为12……
按照以上规律，解决下列问题：

(1)、图6中盆景数量为，盆花数量为；

(2)、已知该生产基地展出以上两种花卉在某种图案中的数量之和为130盆，分别求出该图案中盆景和盆花的数量；

(3)、若有n（n为偶数，且 $n \geq 2$ ）盆盆景需要展出（只摆一种图案），照此组合图案，需要盆花的数量为．（用含n的代数式表示）

查看试题解析
23. 如图，在长方形ABCD中，BC＝20cm，P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在长方形的边上同时运动，当有一个点先到达所在运动边的另一个端点时即停止，已知在相同时间内，若BQ＝xcm（x≠0），则AP＝2xcm，CM＝3xcm，DN＝x²cm．

(1)、当x为何值时，点的运动停止？

(2)、点P与点N可能相遇吗？点Q与点M呢？请通过计算说明理由．

(3)、当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形？

查看试题解析
24. （发现问题）
小聪发现图1所示矩形甲与图2所示矩形乙的周长与面积满足关系： $\frac{C_{乙}}{C_{甲}} = \frac{S_{乙}}{S_{甲}} = \frac{1}{2}$ .

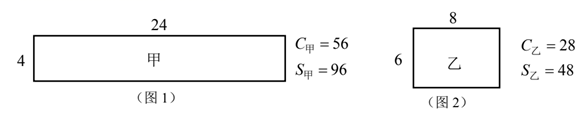
（提出问题）

对于任意一个矩形 $A$ ，是否一定存在矩形 $B$ ，使得 $\frac{C_{B}}{C_{A}} = \frac{S_{B}}{S_{A}} = \frac{1}{2}$ 成立？

（解决问题）

(1)、对于图2所示的矩形乙，是否存在矩形丙（可设两条邻边长分别为 $x$ 和 $7 - x$ ），使得 $\frac{C_{丙}}{C_{乙}} = \frac{S_{丙}}{S_{乙}} = \frac{1}{2}$ 成立.若存在，求出矩形丙的两条邻边长；若不存在，请说明理由；

(2)、矩形 $A$ 两条邻边长分别为 $m$ 和1，若一定存在矩形 $B$ ，使得 $\frac{C_{B}}{C_{A}} = \frac{S_{B}}{S_{A}} = \frac{1}{2}$ 成立，求 $m$ 的取值范围；

(3)、请你回答小聪提出来的问题.若一定存在，请说明理由；若不一定存在，请直接写出矩形 $A$ 两条邻边长 $a ， b$ 满足什么条件时一定存在矩形 $B$ .

查看试题解析