2023年春季北师版数学九年级下册总复习检测A
试卷更新日期:2022-11-26 类型:期末考试
一、单选题(每题3分,共30分)
-
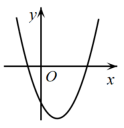
1. 的值等于( )A、2 B、1 C、 D、2. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大3. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
 A、
A、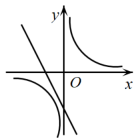 B、
B、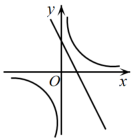 C、
C、 D、
D、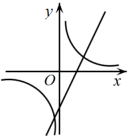 4. 抛物线经平移后,不可能得到的抛物线是( )A、 B、 C、 D、5. 如图,为的直径,弦交于点 , , , , 则( )
4. 抛物线经平移后,不可能得到的抛物线是( )A、 B、 C、 D、5. 如图,为的直径,弦交于点 , , , , 则( )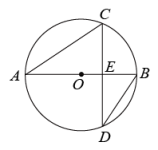 A、 B、 C、1 D、26. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
A、 B、 C、1 D、26. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,垂直地面,垂足为点D, , 垂足为点C.设 , 下列关系式正确的是( )
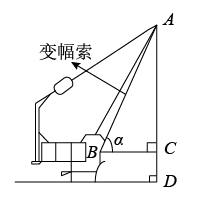 A、 B、 C、 D、7. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )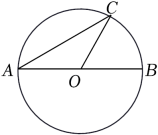 A、6π B、2π C、π D、π8. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )
A、6π B、2π C、π D、π8. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )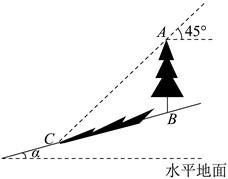 A、 B、 C、 D、9. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )
A、 B、 C、 D、9. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )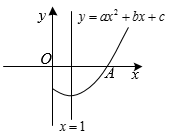 A、1 B、2 C、3 D、410. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、1 B、2 C、3 D、410. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )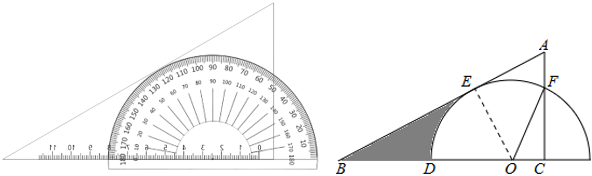 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 在Rt△ABC中,∠C=90°,AC=1,BC= , 则cosA= .12. 根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 , 当飞行时间t为s时,小球达到最高点.13. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.
用公式可描述为:a2=b2+c2﹣2bccosA
b2=a2+c2﹣2accosB
c2=a2+b2﹣2abcosC
现已知在△ABC中,AB=3,AC=4,∠A=60°,则BC= .
14. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .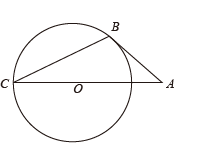 15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).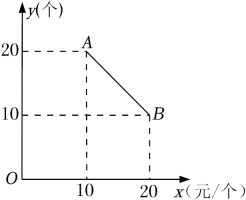 16. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .
16. 如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角 . 则图中阴影部分面积是 .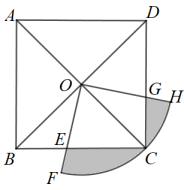
三、解答题(共9题,共72分)
-
17. 计算:.18. 计算:﹣2tan45°+|﹣3|+(π﹣2022)0 .19. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
 (1)、求证: .(2)、若 , , 求阴影部分的面积.20. 随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔 , 小明在坡脚处测得塔顶的仰角为 , 然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角 . (点、、、、均在同一平面内,为地平线)(参考数据: , , )
(1)、求证: .(2)、若 , , 求阴影部分的面积.20. 随着我国科学技术的不断发展,5G移动通信技术日趋完善.某市政府为了实现5G网络全覆盖,2021~2025年拟建设5G基站3000个,如图,在斜坡上有一建成的5G基站塔 , 小明在坡脚处测得塔顶的仰角为 , 然后他沿坡面行走了50米到达处,处离地平面的距离为30米且在处测得塔顶的仰角 . (点、、、、均在同一平面内,为地平线)(参考数据: , , ) (1)、求坡面的坡度;(2)、求基站塔的高.21. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .
(1)、求坡面的坡度;(2)、求基站塔的高.21. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .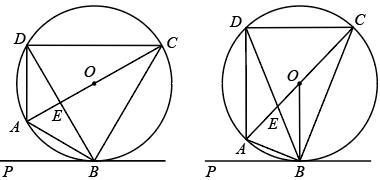 (1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .22. 某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y(单位:人)与时间x(单位:分钟)的变化情况,发现其变化规律符合函数关系式:数据如下表.
(1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .22. 某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y(单位:人)与时间x(单位:分钟)的变化情况,发现其变化规律符合函数关系式:数据如下表.时间x(分钟)
0
1
2
3
…
8
累计人数y(人)
0
150
280
390
…
640
640
(1)、求a,b,c的值;(2)、如果学生一进入操场就开始排队进行核酸检测,检测点有4个,每个检测点每分钟检测5人,求排队人数的最大值(排队人数-累计人数-已检测人数);(3)、在(2)的条件下,全部学生都完成核酸检测需要多少时间?如果要在不超过20分钟让全部学生完成核酸检测,从一开始就应该至少增加几个检测点?23. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.(参考数据: , )
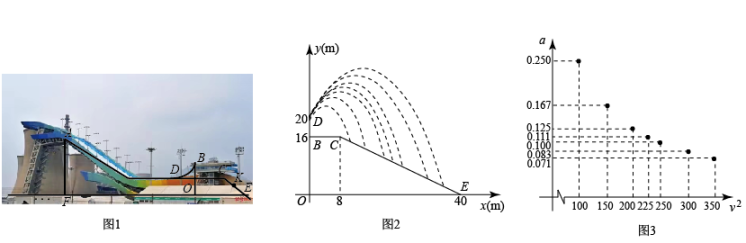 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?
24. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
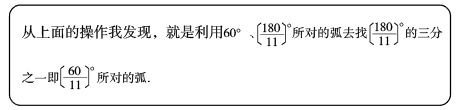
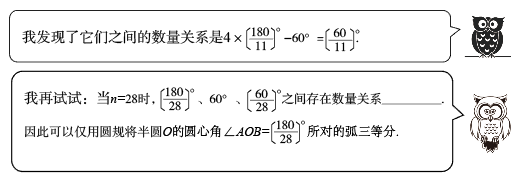
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)、如图2,的圆周角 . 为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).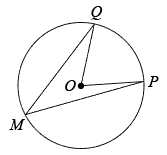 25. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
25. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.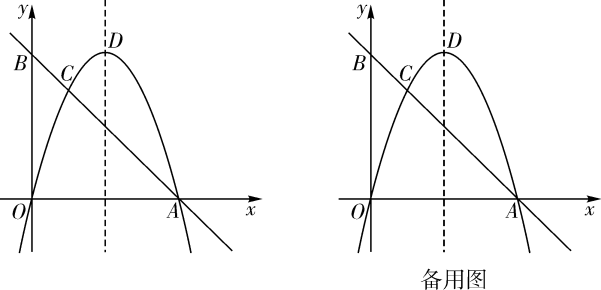 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.