浙教版备考2023年中考数学一轮复习16.一元一次方程的应用（2）

试卷更新日期：2022-11-26 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 2022年2月6日女足亚洲杯决赛，在逆境中铿锵玫瑰没有放弃，逆转夺冠！某学校掀起一股足球热，举行了班级联赛，某班开局11场保持不败，积23分，按比赛规则，胜一场得3分，平一场得1分，则该班获胜的场数为（）

A、4 B、5 C、6 D、7

查看试题解析
2. 医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表．某人住院治疗后得到保险公司报销金额是1100元，那么此人住院的医疗费是（）
住院医疗费（元）
报销率（%）
不超过500元的部分
0
超过500～1000元的部分
60
超过1000～3000元的部分
80
……

A、1000元 B、1250元 C、1500元 D、2000元

查看试题解析
3. 我国“DF－41型”导弹俗称“东风快递”，速度可达到26马赫（1马赫＝340米/秒），则“DF－41型”导弹飞行多少分钟能打击到12000公里处的目标？设飞行 $x$ 分钟能打击到目标，可以得到方程（）

A、 $26 \times 340 \times 60 x = 12000$ B、 $26 \times 340 x = 12000$ C、 $\frac{26 \times 340 x}{1000} = 12000$ D、 $\frac{26 \times 340 \times 60 x}{1000} = 12000$

查看试题解析
4. 周末，小明的妈妈让他到药店购买口罩和酒精湿巾，已知口罩每包3元，酒精湿巾每包2元，共用了30元钱（两种物品都买），小明的购买方案共有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
5. 某商店有两个进价不同的计算器都卖了a元，其中一个盈利60%，另一个亏本20%，在这次买卖中，这家商店是（）

A、盈利了 B、亏本了 C、既不盈利，也不亏损 D、无法判断

查看试题解析
6. 为了更有效地展开体育锻炼，某班将参加体育锻炼的同学进行分组，如果每组8人，则多余4人；如果每组10人，则还缺6人，若参加体育锻炼的有x人，则下列所列方程中正确的是（）

A、 $8 x + 4 = 10 x - 6$ B、 $8 x - 4 = 10 x + 6$ C、 $\frac{x - 4}{8} = \frac{x + 6}{10}$ D、 $\frac{x + 4}{8} = \frac{x - 6}{10}$

查看试题解析
7. 新华书店推出售书优惠方案：①一次性购书不超过100元，不享受优惠；②一次性购书超过100元但不超过200元一律打九折；③一次性购书200元一律打八折．如果小明同学一次性购书付款162元，那么小明所购书的原价为（）

A、180元 B、202.5元 C、180元或202.5元 D、180元或200元

查看试题解析
8. 如图是某公园在一长35m，宽23m的矩形湖面上修建的等宽的人行观景曲桥，它的面积恰好为原矩形湖面面积的 $\frac{1}{5}$ ，求人行观景曲桥的宽．若设人行观景曲桥的宽为xm，则x满足的方程为（）

A、 $(35 - 2 x) (23 - x) = \frac{1}{5} \times 23 \times 35$ B、 $(35 - x) (23 - x) + 2 x^{2} = 23 \times 35$ C、 $(35 - x) (23 - x) = \frac{4}{5} \times 23 \times 35$ D、 $(35 - x) (23 - x) = 23 \times 35$

查看试题解析
9. 某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在100元（不含100元）以内，不享受优惠；②一次性购物在100元（含100元）以上，350元（不含350元）以内，一律享受九折优惠；③一次性购物在350元（含350元）以上，一律享受八折优惠；小敏在该超市两次购物分别付了85元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元

A、284 B、308 C、312 D、320

查看试题解析
10. 某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在 $100$ 元（不含 $100$ 元）以内，不享受优惠；
②一次性购物在 $100$ 元（含 $100$ 元）以上， $350$ 元（不含 $350$ 元）以内，一律享受九折优惠；
③一次性购物在 $350$ 元（含 $350$ 元）以上，一律享受八折优惠；
小敏在该超市两次购物分别付了90 元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元

A、 $288$ B、 $296$ C、 $312$ D、 $320$

查看试题解析

二、填空题（每题4分，共24分）

11. 2022年5月10日，天舟四号货运飞船成功发射．在此之际，某校组织了一次航天科普知识竞赛，一共有25道题，规定答对一题得10分，答错（或不答）一题扣5分．小明同学的成绩超过100分，则他至少答对道题．

查看试题解析

12. 下表是某市居民出行方式以及收费标准：（不足1千米按1千米算）

打车方式	出租车	3千米以内8元；超过3千米的部分2.4元/千米
打车方式	滴滴快车	路程：1.4元/千米；时间：0.6元/分钟
说明	打车的平均车速40千米/时

假设乘坐8千米，耗时：8÷40×60＝12分钟；出租车收费：8＋（8－3）×2.4＝20元；滴滴快车收费：8×1.4＋12×0.6＝18.4元．

为了提升市场竞争力，出租车公司推出行使里程超过10千米立减4.8元活动．小聪乘坐出租车从甲地到达乙地支付车费22.4元，若改乘滴滴快车从甲地到乙地，则需支付元．

查看试题解析

13. 已知点O是数轴的原点，点A、B、C在数轴上对应的数分别是﹣12、b、c ，且b、c满足（b﹣9）²+|c﹣15|＝0，动点P从点A出发以2单位/秒的速度向右运动，同时点Q从点C出发，以1个单位/秒速度向左运动，O、B两点之间为“变速区”，规则为从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速，从点B运动到点O期间速度变为原来的3倍，之后立刻恢复原速，运动时间为秒时，P、Q两点到点B的距离相等．

查看试题解析
14. 七年级某班准备组织同学们观看电影，由班长负责买票，已知电影票价每张50元，对观影人数超过40人的团体票有两个优惠方案可选择：方案一：全体人员可打8折；方案二：若有5人免票，则其他人可以打9折．班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的．若这个班级观影人数超过40人，则该班共有人观看电影．

查看试题解析
15. 某商场在“庆元旦”的活动中将某件服装打折销售，如果这件服装按标价的50%出售将亏30元，而按标价的80%出售将赚30元，则这件服装的进价是元.

查看试题解析
16. 如果等腰三角形的周长是27cm，一腰上的中线把三角形分成两个三角形，其周长之差是3cm，则这个等腰三角形的底边长为cm。

查看试题解析

三、解答题（共8题，共66分）

17. 某电视台组织知识竞赛，共设20道选择题，各题分值相同、每题必答，下表记录了五位参赛者的得分情况．根据表格提供的信息解答下列问题：
参赛者
A
B
C
D
E
答对题数
20
19
18
14
m
得分
100
94
88
n
40

(1)、每做对一题得分，每做错一题得分；

(2)、直接写出 $m =$ ， $n =$ ；

(3)、参赛者G说他得了80分，你认为可能吗?为什么?

查看试题解析
18. 为了加强公民的节水意识，合理利用水资源.某市采用阶梯价格调控手段达到节水目的，价目表如图．

(1)、若某户居民1月份用水8 m³ ，则水费元；

(2)、若某户居民某月用水x m³ ，则用含x的代数式表示水费；

(3)、若某户居民3、4月份共用水15 m³ ，（4月份用水量超过3月份），共交水费44元，则该户居民3、4月份各用水多少立方米？

查看试题解析
19. 如图，数轴上点A表示的数为-3，点B表示的数为4，阅读并解决相应问题．

(1)、问题发现：若在数轴上存在一点P，使得点P到点A的距离与点P到点B的距离之和等于n，则称点P为点A、B的“n节点”．如图1，若点P表示的数为1，点P到点A的距离与点P到点B的距离之和为4+3=7，则称点P为点A、B的“7节点”．
填空：
①若点P表示的数为 $- 2$ ，则n的值为；
②数轴上表示整数的点称为整点，若整点P为A、B的“7节点”，则这样的整点P共有个．

(2)、类比探究：如图2，若点P为数轴上一点，且点P到点A的距离为1，请你求出点P表示的数及n的值．

(3)、拓展延伸：若点P在数轴上运动 $($ 不与点A、B重合 $)$ ，满足点P到点B的距离等于点P到点A的距离的 $\frac{3}{4}$ ，且此时点P为点A、B的“n的节点”，请写出点P表示的数及n的值．

查看试题解析
20. 下面的两种移动电话计费方式表，考虑下列问题：

方式一
方式二
月租费
20元/月
25元/月
通话费
0.25元/分
0.2元/分

(1)、某用户某月打手机x小时，请你写出两种方式下该用户应交付的费用；

(2)、若某用户估计一个月内打手机时间为150分钟，你认为采用哪种方式更合算?

(3)、通话多长时间两种方式付费相同？

查看试题解析
21. 某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物．如果每人制作9个，那么就比计划少做17个；如果每人制作12个，那么就比计划多做4个．

(1)、这个手工兴趣小组共有多少人？计划要做的这批中国结有多少个？

(2)、同学们打算用A，B两种不同的编结方式来制作这一批中国结，已知每个A型中国结需用红绳0.6米，每个B型中国结需用红绳0.9米，现有50米红绳，制作这批中国结能恰好用完这50米红绳吗？请说明你的理由．

查看试题解析
22. 第24届冬季奥林匹克运动会将于2022年2月4日至2022年2月20日在北京市和张家口市联合举行，北京是唯一一个既举办冬季奥运会又举办夏季奥运会的城市.为了迎接2022年北京冬季奥运会，某校准备举行冬季长跑比赛，为奖励长跑优胜者，学校需要购买一些冬奥会吉祥物冰墩墩、雪容融中性笔和徽章.了解到某商店中性笔的单价比徽章的单价多11元，若买2支中性笔和3个徽章共需67元.

(1)、中性笔和徽章的单价各是多少元？

(2)、该商店推出两种优惠方案，方案一：消费金额超过200元的部分打八折；方案二：全店商品打九折.若学校需要购买10支中性笔和30个徽章，选择哪种方案更优惠？

查看试题解析
23. 如图为半圆形计时器，指针 $O M$ 绕点 $O$ 从 $O B$ 开始逆时针向 $O A$ 旋转，速度为 $5^{0}$ 每秒，指针 $O N$ 绕点 $O$ 从 $O A$ 开始先顺时针向 $O B$ 旋转，到达 $O B$ 后再逆时针向回旋转，速度为 $10^{\circ}$ 每秒，两指针同时从起始位置出发，当 $O M$ 到达时，两针都停止旋转。设旋转时间为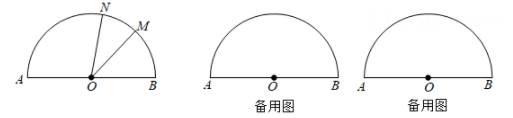 $t$ 秒

(1)、求 $t$ 为何值时 $O M$ 与 $O N$ 首次重合；

(2)、求 $∠ M O N$ (用含 $t$ 的代数式表示)；

(3)、直接写出 $∠ B O N = 2 ∠ M O N$ 时 $t$ 的值为.

查看试题解析
24. 阅读理解：在钟面上，把一周分成12个大格，每个大格分成5个小格，所以每个大格对应的是30°角，每个小格对应的是6°角，时针每分钟转过的角度是0.5度，分针每分针转过的角度是6度.
解决问题：

(1)、当时钟的时刻是8：30时，求此时分针与时针所夹的锐角的度数.

(2)、8：00开始几分钟后分针第一次追上时针.

(3)、设在8：00时，分针的位置为OA，时针的位置为OB，运动后的分针为OP，时针为OQ.问：在8：00～9：00之间，从8：00开始运动几分钟，OB，OP，OQ这三条射线，其中一条射线是另外两条射线所夹的角的平分线？

查看试题解析

住院医疗费（元）	报销率（%）
不超过500元的部分	0
超过500～1000元的部分	60
超过1000～3000元的部分	80
……

	方式一	方式二
月租费	20元/月	25元/月
通话费	0.25元/分	0.2元/分

参赛者	A	B	C	D	E
答对题数	20	19	18	14	m
得分	100	94	88	n	40