浙教版备考2023年中考数学一轮复习14.等式的性质与方程的认识
试卷更新日期:2022-11-26 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列各式中:①;②;③;④;⑤;⑥ , 是方程的是( )A、①④ B、①②⑤ C、①④⑤ D、①②④⑤2. 关于x的方程是一元一次方程,则这个方程的解是( )A、 B、 C、 D、3. 对于等式: ,下列说法正确的是( )A、不是方程 B、是方程,其解只有2 C、是方程,其解只有0 D、是方程,其解有0和24. 下列方程的解是 的有( )
① ② ③ ④
A、1个 B、2个 C、3 D、4个5. 下列说法正确的是( ).A、x=-2是方程x-2=0的解 B、x=6是方程3x+18=0的解 C、x=-1是方程-=0的解 D、x=是方程10x=1的解6. 下列变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 在一次会议中,每两人都握了一次手,共握手21次,设有x人参加会议,则可列方程为( )A、x(x+1)=21 B、x(x﹣1)=21 C、 D、8. 某超市一月份的营业额为20万元,已知第一季度的总营业额共100万元,如果营业额平均每月的增长率为x,那么由题意列方程应为( )A、 B、 C、 D、9. 某商场将每件进价为20元的玩具以单价为30元的价格出售时,每天可售出300件,经调查当单价每涨1元时,每天少售出10件.若商场想每天获得3750元利润,则每件玩具应涨多少元?这道应用题如果设每件玩具应涨x元,则下列说法错误的是( )A、涨价后每件玩具的售价是(30+x)元 B、涨价后每天少售出玩具的数量是10x件 C、涨价后每天销售玩具的数量是(300﹣10x)件 D、可列方程为(30+x)(300﹣10x)=375010. 在数学活动课上,兴趣小组的同学用一根质地均匀的轻质木杆和若干个钩码做实验.如图所示,在轻质木杆O处用一根细线悬挂,左端A处挂一重物,右端B处挂钩码,每个钩码质量是50g.若OA=20cm,OB=40cm,挂3个钩码可使轻质木杆水平位置平衡.设重物的质量为xg,根据题意列方程得( )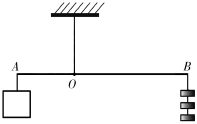 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 观察方程 , , , 的未知数的个数和未知数的次数,从这些方程的共同特征,可以将它们称为 .12. 写出一个关于x的一元一次方程是 .13. 若关于x的方程是一元一次方程,则 .14. 已知关于x的方程的解是 , 则a的值是 .15. 我国的《洛书》中记载着世界最古老的一个幻方:将九个数字填入 的方格中,使三行、三列、两对角线上的三个数之和都相等,根据如图的幻方,则代数式 .
x
-2
y
0
16. 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图所示,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?设生产圆形铁片的工人有人,则生产长方形铁片的工人有人,依题意可列方程为 .
三、解答题(共8题,共66分)
-
17. 下列方程的变形是否正确?为什么?(1)、由3+x=5,得x=5+3.(2)、由7x=﹣4,得x= .(3)、由 ,得y=2.(4)、由3=x﹣2,得x=﹣2﹣3.18. 已知 m﹣1= n,试用等式的性质比较m与n的大小.19. 方程(k2﹣4)x2+(k+2)x+(k﹣6)y=k+8是关于x、y的方程,试问当k为何值时,(1)、方程为一元一次方程?
(2)、方程为二元一次方程?
20. 已知:方程(m+2)x|m|﹣1﹣m=0①是关于x的一元一次方程.(1)、求m的值;(2)、若上述方程①的解与关于x的方程x+=﹣3x②的解互为相反数,求a的值.21. 已知关于 的方程 为一元一次方程,且该方程的解与关于 的方程 的解相同.(1)、求 、 的值;(2)、在(1)的条件下,若关于 的方程 有无数解,求 , 的值.22. 根据下列题干设未知数列方程,并判断它是不是一元一次方程.(1)、从60cm的木条上截去2段同样长的木棒,还剩下10cm长的短木条,截下的每段为多少?(2)、小红对小敏说:“我是6月份出生的,我的年龄的2倍加上10,结果正好是我出生的那个月的总天数,你猜我有几岁?”23. 学校计划购买6张“双鱼”牌乒乓球桌和a副“红双喜”牌乒乓球拍(不少于6副). A、B两家体育商品店的价格相同,球桌每张1000元,球拍每副200元.A店优惠政策是每买一张乒乓球桌,送一副球拍;B店的优惠政策为所有商品打八五折.(1)、规定只能到其中一个店购买乒乓球桌和乒乓球拍,请分别用含a的代数式表示在A、B两家体育商品店购买这些物品所需的费用,并化简.(2)、若到A、B两家店购买,所需费用相等,求a的值.24. 我们规定,若关于x的一元一次方程ax=b的解为x=b-a,则称该方程为“定值方程”.例如:2x=4的解为x=2=4-2,则该方程2x=4是“定值方程”.请根据上述规定解答下列问题:(1)、判断方程4x=6 (回答“是”或“不是”)“定值方程”;(2)、若a=3,有符合要求的“定值方程”吗?若有,求b的值;若没有,请说明理由.(3)、若关于x的一元一次方程2x=mn+m和-2x=mn+n都是“定值方程”, 求代数式5-3m+3n的值.