浙教版备考2023年中考数学一轮复习8.探索数与式的规律
试卷更新日期:2022-11-26 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 若a是不为2的有理数,则我们把称为a的“奇特数”.如:4的“奇特数”是 , 的“奇特数”是.已知 , 是的“奇特数”,是的“奇特数”,是的“奇特数”,…,以此类推,则等于( )A、4 B、 C、 D、2. 观察下列等式: , , , , , , , 试利用上述规律判断算式结果的末位数字是( )A、0 B、1 C、3 D、73. 如图所示,在这个运算程序当中,若开始输入的x是2,则经过2021次输出的结果是( )
 A、1 B、3 C、4 D、84. 规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它关于x轴作对称点,一个点作“2”变换表示将它关于y轴作对称点.由数字0,1,2组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点 按序列“012”作变换,表示点A先向右平移一个单位得到 , 再将关于x轴对称得到 , 再将关于y轴对称得到 ......依次类推.点经过“012012012.......”100次变换后得到点的坐标为( ).(注:“012”算3次变换)
A、1 B、3 C、4 D、84. 规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它关于x轴作对称点,一个点作“2”变换表示将它关于y轴作对称点.由数字0,1,2组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点 按序列“012”作变换,表示点A先向右平移一个单位得到 , 再将关于x轴对称得到 , 再将关于y轴对称得到 ......依次类推.点经过“012012012.......”100次变换后得到点的坐标为( ).(注:“012”算3次变换) A、 B、 C、 D、5. 取一个自然数, 若它是奇数, 则乘以3加上1 , 若它是偶数, 则除以2 , 按此规则经过若干步的计算最终可得1. 这个结论在数学上还没有得到证明, 但举例验证都是正确的. 例如: 取自然数5 , 经过下面5步运算可得1 , 即: 如图所示, 如果自然数恰好经过6步运算可得到1 , 则所有符合条件的的值有( )
A、 B、 C、 D、5. 取一个自然数, 若它是奇数, 则乘以3加上1 , 若它是偶数, 则除以2 , 按此规则经过若干步的计算最终可得1. 这个结论在数学上还没有得到证明, 但举例验证都是正确的. 例如: 取自然数5 , 经过下面5步运算可得1 , 即: 如图所示, 如果自然数恰好经过6步运算可得到1 , 则所有符合条件的的值有( ) A、1 个 B、2 个 C、3 个 D、4 个6. 将正偶数按下表排成5列:
A、1 个 B、2 个 C、3 个 D、4 个6. 将正偶数按下表排成5列:第一列 第2列 第3列 第4列 第5列 第1行 2 4 6 8 第2行 16 14 12 10 第3行 18 20 22 24 …… …… 28 26 根据上面排列规律,则2022应在____________行,___________列.( )
A、506;3 B、506;2 C、253;2 D、253;47. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如 , 仿此,若m3的“分裂数”中有一个是59,则m的值为( )A、6 B、7 C、8 D、98. 《压子》中记载:“一尺之捶,日取其半,万世不竭 .”这句话的意思是一尺长的木棍,每天截取它的一半,永远也截不完.若按此方式截一根长为1的木棍,第1天截取它的一半,第2天截取第1天剩余的一半,以此类推,第5天截取后木棍剩余的长度是( )A、1﹣ B、1﹣ C、 D、9. 按一定规律排列的一组数据: , , , , , , ….则按此规律排列的第10个数是( )A、 B、 C、 D、10. 观察下列等式:第1层
第2层
第3层
第4层
在上述数字宝塔中,从上往下数,2022在第( )层.
A、33 B、34 C、44 D、45二、解答题(共9题,共69分)
-
11. 观察下列等式:9﹣1=2×4,16﹣4=3×4,25﹣9=4×4,36﹣16=5×4,…,这些等式反映自然数间的某种规律,设n表示自然数,请猜想出这个规律,用含n的等式表示出来,并加以证明.12. 判断以下列各式是否成立:
; ; .
类比上述式子,再写出两个同类的式子.你能看出其中的规律吗?用字母表示这一规律,并给出证明.
13. 如果记 , 并且表示当时y的值,即;表示当时y的值,即;…,求的值(结果用含n的代数式表示).14. 观察下面依次排列的一些数:, , , , , , ⋯
猜测排列的规律,并回答下列问题.
(1)、第7个数是 , 第8个数是.(2)、第2023个数是.(3)、如果这列数依据这个规律无限排列下去,与哪个整数越来越接近?直接写出这个整数.15. 观察算式,找规律:;
;
;
;
……
(1)、由以上算式可知: ;(2)、计算: .16. 请先阅读下列一组内容,然后解答问题:因为:
所以:
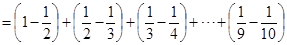
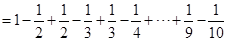
问题:
计算:① ;
②
17. 观察按下列规则排成的一列数; ...(1)、容易发现,从左起第22个数是 , 则它前面的那个数是多少, 后面的那个数是多少?(2)、从左起第个数记为 ,例如 , 则表示的数是多少? 表示的数是多少?(3)、当时, 求值是多少? 并求出这个数的积.18. 已知x≠1.观察下列等式:(1﹣x)1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4
⋯
(1)、猜想:(1﹣x)(1+x+x2+x3+⋯+xn﹣1)=;(2)、应用:根据你的猜想请你计算下列式子的值:①(1﹣2)(1+2+22+23+24+25+26)=;
②(x﹣1)(x222+x2021+x2020+...+x2+x+1)= .
(3)、判断2100+299+298+...+22+2+1的值的个位数是几?并说明你的理由.19. 有一种计算器,输出规则如下:输入两个关于x的整式A,B,对它们进行整式加法运算,若的结果为单项式,则输出该单项式;若的结果为多项式,则输出该多项式的最高次项与最低次项的和.已知输入的整式 .(1)、若 , 则输出结果为;(2)、若输出结果为 , 则整式B应满足什么条件?写出结论,并说明理由;(3)、若将整式A,B输入计算器,得到输出结果,记为第一次运算,然后将输出结果与A再次输入该计算器,得到输出结果,记为第二次运算,……,依次进行上面操作,若第次运算得到的输出结果恰为单项式,请写出一个满足题意的整式B.三、填空题(每题3分,共21分)
-
20. —动点P从数轴上的原点出发,按下列规则运动:①沿数轴的正方向先前进5个单位,然后后退3个单位,如此反复进行.②已知点P每秒只能前进或后退1个单位,设表示第n秒点P在数轴上的位置所对应的数,则为.21. 有一列数按一定的规律排列为-1,3,-5,7,-9,11, , 如果其中三个相邻的数之和为199,那么这三个相邻数中间的数为.22. 小明同学利用计算机设计了一个程序,输入和输出的情况如下表.他发现从第三个输出项起的每一项都与这一项的前面两个输出项有关.按此规律,当输入9时,输出结果为 , 从1开始一直输入到2022后,输出项的系数与次数均为奇数的项共有个.
输入
1
2
3
4
5
6
7
8
…
输出
a
…
23. 《九章算术》中有这样一个问题:“今有蒲生一日,长三尺;蒲生日自半”.其意思是“有蒲这种植物,蒲第一日长了3尺,以后蒲每日生长的长度是前一日的一半”.则第二十日蒲生长的长度为尺.