浙教版备考2023年中考数学一轮复习5.列代数式与代数式求值

试卷更新日期：2022-11-26 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列各代数式中，符合代数式书写规则的是（）

A、 $\frac{1}{2} x^{2}$ B、 $a \times 4$ C、 $- 3 \frac{1}{3} y$ D、 $2 p \div q$

查看试题解析
2. 某商品进价为400元，标价x元，在商场开展的促销活动中，该商品按8折销售，那么该商品仍可以获利（）

A、 $(8 x - 400)$ 元 B、 $(400 \times 8 - x)$ 元 C、 $(0.8 \times 400 - x)$ 元 D、 $(0.8 x - 400)$ 元

查看试题解析
3. 甲数是乙数的2倍少3 ，则下列说法正确的是（）
①设乙数为 $x$ ，甲数为 $2 x - 3$ ②设甲数为 $x$ ，乙数为 $\frac{1}{2} x + 3$ ③设甲数为 $x$ ，乙数为 $\frac{1}{2} (x + 3)$ ④设甲数为 $x$ ，乙数为 $\frac{1}{2} (x - 3)$

A、①③ B、①② C、②④ D、①④

查看试题解析
4. 下列代数式表示正确的是（）

A、a，b两数的平方和：（a+b）² B、a，b两数的差的平方：a²-b² C、y与2的差的两倍：2（y-2） D、m，n两数的倒数和： $\frac{1}{m + n}$

查看试题解析
5. 已知 $A$ 、 $B$ 两地相距100米，甲、乙两人分别从 $A$ 、 $B$ 两地同时出发，相向而行，速度分别为 $x$ 米/秒、 $y$ 米/秒，甲、乙两人第一次相距 $a (a < 100)$ 米时，所用时间为（）

A、 $\frac{100 - a}{x - y}$ 秒 B、 $\frac{100 + a}{x - y}$ 秒 C、 $\frac{100 + a}{x + y}$ 秒 D、 $\frac{100 - a}{x + y}$ 秒

查看试题解析
6. 如图1，将1个长方形沿虚线剪开得到两个长方形，再将这两个长方形拼成图2，则下列等式可以解释两图形面积变化的数量关系的是（　　）

A、 $(x + 3) (x - 2) = x (x + 1) - 6$ B、 ${(x + 3)}^{2} = x (x + 6) + 9$ C、 $(x - 3) (x - 2) = x (x - 5) + 6$ D、 $(x + 3) (x - 3) = x^{2} - 9$

查看试题解析
7. 1.计算 $\overset{m 个}{\overset{︷}{2 + 2 + 2 ⋯ + 2}} + \overset{n 个}{\overset{︷}{3 \times 3 \times 3 ⋯ \times 3}} =$ （）

A、 $2 m + 1$ B、 $m^{2} + 3 n$ C、 $2^{m} + 3 n$ D、 $2 m + 3^{n}$

查看试题解析
8. 已知 $2 x + y + 1 = 10 ，$ 则代数式 $20 + 4 x + 2 y$ 的值为（）．

A、18 B、19 C、20 D、38

查看试题解析
9. 已知实数 $x ， y$ 满足 $| x - 3 | + (y + 4)^{2} = 0$ ，则代数式 $(x + y)^{2020}$ 的值为（）

A、1 B、-1 C、2020 D、-2020

查看试题解析
10. 乐乐在数学学习中遇到了神奇的“数值转换机”，按如图所示的程序运算，若输入一个有理数x，则可相应的输出一个结果y．若输入x的值为-1，则输出的结果y为（）

A、 $- 5$ B、7 C、10 D、12

查看试题解析

二、解答题（共8题，共66分）

11. 如果a，b互为倒数，c，d互为相反数，且m的绝对值是2，求代数式2ab-（c+d）-m的值．

查看试题解析
12. 底面为正方形的长方体，体积为 $32 {cm}^{3}$ ，底面边长为 $x (cm)$ ，请用含 $x$ 的式子表示这个长方体的高 $h (cm)$ ，并求当底面边长为 $2 cm$ 时 $h$ 的值.

查看试题解析
13. 如图，有长、宽分别为 $a$ 、 $b$ 的长方形一个和三边长分别为 $a$ 、 $b$ 、c的直角三角形两个.请你用这三个图形无缝拼成新的四边形，并直接写出形状不同的四边形的周长.(要求画出示意图形)

查看试题解析
14. 如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”(如图2)，得到大小两个正方形，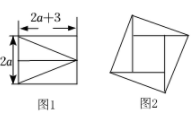

(1)、用关于a的代数式表示图2中小正方形的边长

(2)、当a=3时，该小正方形的面积是多少？

查看试题解析
15. 已知三角形的三边长分别为a，b，c，求其面积，古希腊的几何学家海伦给出海伦公式 $S = \sqrt{p (p - a) (p - b) (p - c)}$ （其中 $p = \frac{a + b + c}{2}$ ），我国南宋时期数学教秦九昭提出了秦九昭公式 $S = \frac{1}{2} \sqrt{a^{2} b^{2} - (\frac{a^{2} + b^{2} - c^{2}}{2})}$ ，若一个三角形的三边长分别为2，2，3，请你选择自己喜欢的公式计算这个三角形的面积.

查看试题解析
16. 某农户承包荒山若干亩，某季度水果总产量为18000千克，种植总成本为8200元.该农户拉到市场出售，平均每天出售1000千克，每千克可售a元，农用车运费及其他各项税费平均每天100元；若在果园出售，每千克售b元（ $b < a$ ），无需农用车运费及其他各项税费.

(1)、分别用a，b表示在市场出售和在果园出售水果的获利情况.

(2)、若 $a = 1.3$ 元， $b = 1.1$ 元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好.

查看试题解析
17. 如图所示，某数学活动小组用计算机编程编制了一个程序进行有理数混合运算，即输入一个有理数，按照程序顺序运算，可输出计算结果，其中“ $□$ ”表示一个有理数．

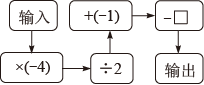(1)、已知 $□$ 表示3．
①若输入的数为－3，求输出结果；
②若输出的数为12，求输入的数．

(2)、若输入的数为 $a$ ， $□$ 表示数 $b$ ，当输出结果为0时，用 $a$ 表示 $b$ 的式子为：．

查看试题解析

18. 如图，一扇窗户，所有窗框为铝合金材料，其下部是边长相同的四个小正方形，上部是半圆形，已知下部小正方形的边长是a米，窗户半圆部分安装彩色玻璃，四个正方形部分安装透明玻璃（本题中π取3，长度单位为米）．

(1)、一扇这样窗户一共需要铝合金多少米？（用含a的代数式表示）

(2)、一扇这样窗户需要彩色和透明玻璃一共多少平方米？（用含a的代数式表示，铝合金窗框宽度忽略不计）

(3)、某公司需要购进10扇窗户，在同等质量的前提下，甲、乙两个厂商分别给出如下报价：

铝合金（米/元）

彩色玻璃（平方米/元）

透明玻璃（平方米/元）

甲厂商

200

不超过100平方米的部分，90元/平方米，

超过100平方米的部分，70元/平方米

乙厂商

220

80元/平方米，每购1平方米透明玻璃送0.1米铝合金

当 $a = 1$ 时，请通过计算说明该公司在哪家厂商购买窗户划算？

查看试题解析

三、填空题（每题4分，共24分）

19. 请根据下面的文字语言，写出相应的代数式或者举出一个符合文字语言的式子来说明.

(1)、x的3倍除以 $y$ 的4倍所得的商：；（代数式）

(2)、m与 $n$ 的差的平方根：；（代数式）

(3)、两个无理数的和为有理数：；（符合文字语言的式子）

(4)、三数相加，和小于其中两个加数，大于第三个加数：.（符合文字语言的式子）

查看试题解析
20. 长方形的长为x厘米，宽比长少2厘米，请列式表示出长方形的面积：平方厘米（结果不需要化简）．

查看试题解析
21. 如图，有一种塑料杯子的高度是10cm，两个以及三个这种杯子叠放时高度如图所示，第 $n$ 个这种杯子叠放在一起高度是cm（用含 $n$ 的式子表示）．

查看试题解析
22. 如图1，在一块长方形区域中布置了图中阴影部分所示的展区，其中的展台有三种不同的形状，其规格如图2所示．

(1)、该长方形区域的长可以用式子表示为；

(2)、根据图中信息，用等式表示a，b，c满足的关系为．

查看试题解析
23. 如图，一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水，将瓶盖盖好后倒置，墨水水面高为h厘米，则瓶内的墨水的体积约占玻璃瓶容积的．

查看试题解析
24. 一个长方形的长与宽分别为a，b，若周长为12，面积为5，则 $a b^{3} + 2 a^{2} b^{2} + a^{3} b$ 的值为．

查看试题解析