浙教版备考2023年中考数学一轮复习4.实数及其运算

试卷更新日期：2022-11-26 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在下列各数中： $π$ ， $- \sqrt{3}$ ， $3.1416$ ， $\sqrt[3]{8}$ ， $\frac{22}{7}$ ，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. $\sqrt{\frac{1}{16}}$ 的算术平方根是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{8}$ D、 $\pm \frac{1}{2}$

查看试题解析
3. $- \sqrt{7}$ 的绝对值是（）

A、 $- \sqrt{7}$ B、 $\sqrt{7}$ C、 $- \frac{\sqrt{7}}{7}$ D、 $\frac{\sqrt{7}}{7}$

查看试题解析
4. 在下列各组数中，互为相反数的一组是（）

A、 $- 2$ 和 $\sqrt[3]{- 8}$ B、 $- 2$ 与 $- \frac{1}{2}$ C、 $- | - \sqrt{2} |$ 和 $\sqrt{2}$ D、 $2$ 和 $\sqrt{{(- 2)}^{2}}$

查看试题解析
5. 在实数0， $\frac{1}{3}$ ， $- \sqrt{17}$ ， $\sqrt{15}$ 中，最大的是（）

A、0 B、 $\frac{1}{3}$ C、 $- \sqrt{17}$ D、 $\sqrt{15}$

查看试题解析
6. 若有理数 $x$ ， $y$ 满足 $y = \sqrt{x - 2} + \sqrt{2 - x} + 1$ ，则 $x - y$ 的平方根是（）

A、 $1$ B、 $\pm 1$ C、 $- 1$ D、无法确定

查看试题解析
7. 如果 $\sqrt[3]{2.37} \approx 1.333$ ， $\sqrt[3]{23.7} \approx 2.872$ ，那么 $\sqrt[3]{23700}$ 约等于（）．

A、28.72 B、287.2 C、13.33 D、133.3

查看试题解析
8. 大于-2.5而小于 $\sqrt{10}$ 的整数共有（）

A、6个 B、5个 C、4个 D、3个

查看试题解析
9. 如图，数轴上有O ， A ， B ， C ， D五点，根据图中各点所表示的数，表示数 $\sqrt{17}$ 的点会落在（）

A、点O和A之间 B、点A和B之间 C、点B和C之间 D、点C和D之间

查看试题解析
10. 下列说法中：①立方根等于本身的是-1，0，1；②平方根等于本身的数是0，1；③两个无理数的和一定是无理数；④实数与数轴上的点是一一对应的；⑤a与b两数的平方和表示为 $a^{2} + b^{2}$ .其中错误的是（）

A、①② B、②③ C、②③④ D、③④⑤

查看试题解析

二、填空题

11. 对于实数 $a 、 b$ ，定义 $m i n {a ， b}$ 的含义为∶ 当 $a < b$ 时， $m i n {a ， b} = a$ ；当 $a > b$ 时， $m i n {a ， b} = b$ ，例如∶ $m i n {1 ， - 2} = - 2$ .已知 $m i n {\sqrt{30} ， a} = a ， m i n {\sqrt{30} ， b} = \sqrt{30}$ ，且 $a$ 和 $b$ 为两个连续正整数，则 $2 a - b$ 的值为.

查看试题解析
12. 下列说法：①任何无理数都是无限不循环小数；②实数与数轴上的点一一对应；③在1和3之间的无理数有且只有 $\sqrt{2} ， \sqrt{3} ， \sqrt{5} ， \sqrt{7}$ 这4个；④近似数1.50所表示的准确数 $x$ 的取值范围是 $1.495 < x < 1.505$ ；⑤a、b互为相反数，则 $\frac{a}{b} = - 1$ ．其中正确的是． (填写序号)

查看试题解析

三、解答题

13. 在数轴上表示下列各数，并用“＜”连接．
$- \frac{1}{2}$ ， 0， $\sqrt{3}$ ， $\sqrt[3]{- 8}$ ， $(- 1)^{2}$

查看试题解析
14. 已知一个正数的平方根分别是2a﹣7和a﹣8，3a﹣b﹣1的立方根为2．

(1)、求6a+b的算术平方根；

(2)、若c是 $\sqrt{13}$ 的整数部分，求2a+3b﹣c的平方根．

查看试题解析
15.

(1)、用“<”“>”或“=”填空： $\sqrt{3}$ $\sqrt{4}$ ， $\sqrt{5}$ $\sqrt{6}$ ；

(2)、由以上可知：① $| \sqrt{16} - \sqrt{17} | =$ ， ② $∣ \sqrt{n - 1} - \sqrt{n} ∣ =$ ；

(3)、计算： $| 1 - \sqrt{2} | + | \sqrt{2} - \sqrt{3} | + | \sqrt{3} - \sqrt{4} | + ⋯ + | \sqrt{n} - \sqrt{n + 1} |$ ．（结果保留根号）

查看试题解析
16. 观察下边图形，每个小正方形的边长为1.

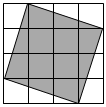(1)、则图中阴影部分的面积是，边长是.

(2)、已知阴影正方形的边长为 $x$ ，且 $a < x < b$ ，若 $a$ 和 $b$ 是相邻的两个整数，那么 $a =$ ， $b =$ .

(3)、若设如图阴影正方形的边长为 $x$ ，请在下面的数轴上准确地作出数 $x$ 所表示的点，若还有一个点 $B$ 与它的距离为1，则这个点 $B$ 在数轴上所表示的数为.

查看试题解析
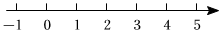17. 阅读下面的文字，解答问题，大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1 ，将这个数减去其整数部分，差就是小数部分，又例如： $∵ 2^{2} < 7 < 3^{2}$ ，即 $2 < \sqrt{7} < 3 ， ∴ \sqrt{7}$ 的整数部分是2 ，小数部分是 $\sqrt{7} - 2 ．$

(1)、请解答： $\sqrt{13}$ 的整数部分是，小数部分是．

(2)、如果 $\sqrt{5}$ 的小数部分是 $a ， \sqrt{29}$ 的整数部分是 $b$ ，求 $a + b - \sqrt{5}$ 的值．

(3)、已知： $x$ 是 $5 + \sqrt{13}$ 的整数部分， $y$ 是其小数部分，求 $x - y$ 的值．

查看试题解析
18. 数形结合是一种重要的数学方法，如在化简 $| a |$ 时，当a在数轴上位于原点的右侧时， $| a | = a$ ；当a在数轴上位于原点时， $| a | = 0$ ；当 $a$ 在数轴上位于原点的左侧时， $| a | = - a$ ．当a，b，c三个数在数轴上的位置如图所示，试用这种方法解决下列问题，

(1)、当 $a = 1$ 时，求 $\frac{| a |}{a} =$ ，当 $b = - 2$ 时，求 $\frac{| b |}{b} =$ ．

(2)、请根据a，b，c三个数在数轴上的位置，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值．

(3)、请根据a，b，c三个数在数轴上的位置，化简： $| a + c | + | c | + | a + b | - | b - c |$ ．

查看试题解析