2023年春季湘教版数学九年级下册第四章《概率》单元检测A

试卷更新日期：2022-11-25 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 一个布袋中放着6个黑球和18个红球，除了颜色以外没有任何其他区别.则从布袋中任取1个球，取出黑球的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析

2. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干，这些糖果除颜色外无其他差别.具体情况如下表所示.

袋子糖果	红色	黄色	绿色	总计
甲袋	2颗	2颗	1颗	5颗
乙袋	4颗	2颗	4颗	10颗

若小明从甲、乙两个袋子中各随机摸出一颗糖果，则他从甲袋比从乙袋（）

A、摸出红色糖果的概率大 B、摸出红色糖果的概率小 C、摸出黄色糖果的概率大 D、摸出黄色糖果的概率小

查看试题解析

3. 下列说法正确的是（）

A、自然现象中，“太阳东方升起”是必然事件 B、成语“水中捞月”所描述的事件，是随机事件 C、“襄阳明天降雨的概率为0.6”，表示襄阳明天一定降雨 D、若抽奖活动的中奖概率为 $\frac{1}{50}$ ，则抽奖50次必中奖1次

查看试题解析
4. 下列说法正确的是（）

A、为了解近十年全国初中生的肥胖人数变化趋势，采用扇形统计图最合适 B、“煮熟的鸭子飞了”是一个随机事件 C、一组数据的中位数可能有两个 D、为了解我省中学生的睡眠情况，应采用抽样调查的方式

查看试题解析
5. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上，若飞镖落在镖盘上各点的机会相等，则飞镖落在阴影区域的概率为（）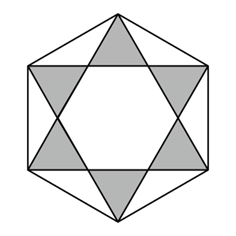

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
6. 如图，正方形 $A B C D$ 及其内切圆 $O$ ，随机地往正方形内投一粒米，落在阴影部分的概率是（）

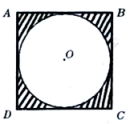A、 $\frac{π}{4}$ B、 $1 - \frac{π}{4}$ C、 $\frac{π}{8}$ D、 $1 - \frac{π}{8}$

查看试题解析
7. 不透明袋中装有除颜色外完全相同的 $a$ 个白球、 $b$ 个红球，则任意摸出一个球是红球的概率是（）

A、 $\frac{b}{a + b}$ B、 $\frac{b}{a}$ C、 $\frac{a}{a + b}$ D、 $\frac{a}{b}$

查看试题解析
8. 从1，2，3，4，5这五个数中任选两个数，其和为偶数的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 为了解某地区九年级男生的身高情况，随机抽取了该地区1000名九年级男生的身高数据，统计结果如下.

身高 $x / cm$

$x < 160$

$160 \leq x < 170$

$170 \leq x < 180$

$x \geq 180$

人数

60

260

550

130

根据以上统计结果，随机抽取该地区一名九年级男生，估计他的身高不低于 $170 cm$ 的概率是（）

A、0.32 B、0.55 C、0.68 D、0.87

查看试题解析
10. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表：

抛掷次数

100

200

300

400

500

正面朝上的频数

53

98

156

202

244

若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（）

A、20 B、300 C、500 D、800

查看试题解析

二、填空题（每空3分，共18分）

11. 在一个不透明的盒子中装有红球和白球共20个，这些球除颜色外无其它差别，随机从盒子中摸出一个球，记下球的颜色后，放回并摇匀．通过大量的实验后发现摸出白球的频率稳定在0.4，则盒子中白球大约有个．

查看试题解析
12. 从2021、2022、2023、2024、2025这五个数中任意抽取3个数．抽到中位数是2022的3个数的概率等于．

查看试题解析
13. 将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人，已知甲有5张红桃牌，乙有4张红桃牌，那么丁的红桃牌有种不同的情况．

查看试题解析
14. 某校围绕习近平总书记在庆祝中国共产主义青年团成立100周年大会上的重要讲话精神，开展了主题为“我叫中国青年”的线上演讲活动．九年级（1）班共有50人，其中男生有26人，现从中随机抽取1人参加该活动，恰好抽中男生的概率是．

查看试题解析
15. 如果小球在如图所示的地板上自由地滚动，并随机的停留在某块方砖上，那么它最终停留在阴影区域的概率是．

查看试题解析
16. 在数学实践课上，同学们进行投针试验：在平面上有一组平行线，相邻两条平行线间的距离都为5cm，将一根长度为3cm的针任意投掷在这个平面上，针可能与某一直线相交，也可能与任一直线都不相交，下表记录了他们的试验数据．
试验次数n
50
100
200
500
1000
2000
相交频数m
23
48
83
207
404
802
相交频率 $\frac{m}{n}$
0.460
0.480
0.415
0.414
0.404
0.401
若进行一次投针试验，估计针与直线相交的概率是（结果保留小数点后一位）．

查看试题解析

三、解答题（共8题，共72分）

17. 某社区举行新冠疫情防控核酸检测大演练，卫生防疫部门在该社区设置了三个核酸检测点A、B、C，甲、乙两人任意选择一个检测点参加检测．求甲、乙两人不在同一检测点参加检测的概率．（用画树状图或列表的方法求解）

查看试题解析
18. 即将在泰州举办的江苏省第20届运动会带动了我市的全民体育热，小明去某体育馆锻炼，该体育馆有A、B两个进馆通道和C、D、E三个出馆通道，从进馆通道进馆的可能性相同，从出馆通道出馆的可能性也相同.用列表或画树状图的方法，列出小明一次经过进馆通道与出馆通道的所有等可能的结果，并求他恰好经过通道A与通道D的概率.

查看试题解析
19. 如图，不透明的管中放置着三根完全相同的绳子AA₁、BB₁、CC₁.在不看的情况下，小明从左端A、B、C三个绳头中随机选一个绳头，小刚从右端A₁、B₁、C₁三个绳头中随机选一个绳头，用画树状图（或列表）的方法，求小明和小刚选中的两个绳头恰好是同一根绳子的概率.

查看试题解析
20. 某中学为了解学生每学期诵读经典的情况，在全校范围内随机抽查了部分学生上一学期阅读量，学校将阅读量分成优秀、良好、较好、一般四个等级，绘制如下统计表：
等级
一般
较好
良好
优秀
阅读量/本
3
4
5
6
频数
12
a
14
4
频率
0.24
0.40
b
c
请根据统计表中提供的信息，解答下列问题：

(1)、本次调查一共随机抽取了名学生；表中 $a =$ ， $b =$ ， $c =$ ．

(2)、求所抽查学生阅读量的众数和平均数．

(3)、样本数据中优秀等级学生有4人，其中仅有1名男生．现从中任选派2名学生去参加读书分享会，请用树状图法或列表法求所选2名同学中有男生的概率

查看试题解析

21. 为了调查九年级学生寒假期间平均每天观看冬奥会时长情况，随机抽取部分学生进行调查，根据收集的数据绘制了如图所示两幅不完整的统计图

“平均每天观看冬奥会时长”频数分布表

观看时长（分）	频数（人）	频率
0＜x≤15	2	0.05
15＜x≤30	6	0.15
30＜x≤45	18	a
45＜x≤60		0.25
60＜x≤75	4	0.1

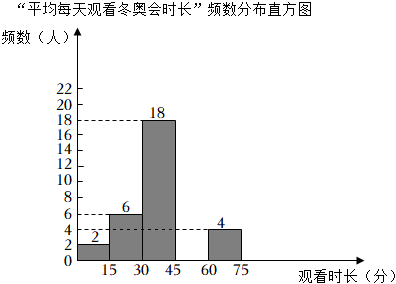(1)、频数分布表中，a＝ ▲ ，请将频数分布直方图补充完整；

(2)、九年级共有520名学生，请你根据频数分布表，估计九年级学生平均每天观看冬奥会时长超过60分钟的有人；

(3)、校学生会拟在甲、乙、丙、丁四名同学中，随机抽取两名同学做“我与冬奥”主题演讲，请用树状图或列表法求恰好抽到甲、乙两名同学的概率．

查看试题解析

22. 神舟十四号载人飞船的成功发射，再次引发校园科技热．光明中学准备举办“我的航天梦”科技活动周，在全校范围内邀请有兴趣的学生参加以下四项活动，A：航模制作；B：航天资料收集；C：航天知识竞赛；D：参观科学馆．为了了解学生对这四项活动的参与意愿，学校随机调查了该校有兴趣的m名学生（每名学生必选一项且只能选择一项），并将调查的结果绘制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：

(1)、 $m =$ ▲ ， $n =$ ▲ ；并补全条形统计图：

(2)、根据抽样调查的结果，请估算全校1800名学生中，大约有多少人选择参观科学馆；

(3)、在选择A项活动的10人中，有甲、乙、丙、丁四名女生，现计划把这10名学生平均分成两组进行培训，每组各有两名女生，则甲、乙被分在同一组的概率是多少？

查看试题解析
23. 为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
教职工气排球比赛比分胜负表

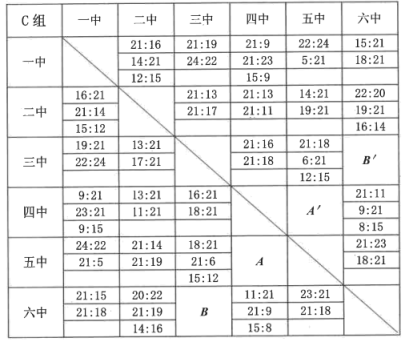(1)、根据表中数据可知，一中共获胜场，“四中VS五中”的比赛获胜可能性最大的是；

(2)、若 $A$ 处的比分是21∶10和21∶8，并且参加决赛的队伍是二中和五中，则 $B^{'}$ 处的比分可以是和；（两局结束比赛，根据自己的理解填写比分）；

(3)、若 $A^{'}$ 处的比分是10∶21和8∶21， $B$ 处的比分是21∶18，15∶21，15∶12，那么实力最强的是哪两支队伍，请说明理由．

查看试题解析
24. 为提高学生的综合素养，某校开设了四个兴趣小组，A“健美操”、B“跳绳”、C“剪纸”、D“书法”为了了解学生对每个兴趣小组的喜爱情况，随机抽取了部分同学进行调查，并将调查结果绘制出上面不完整的统计图，请结合图中的信息解答下列问题：

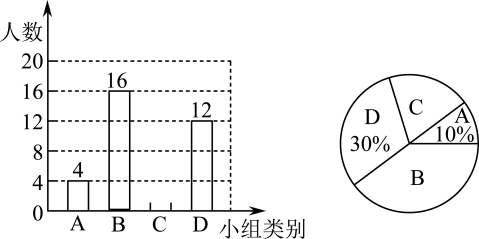(1)、本次共调查了 ▲ 名学生；并将条形统计图补充完整；

(2)、C组所对应的扇形圆心角为度；

(3)、若该校共有学生1400人，则估计该校喜欢跳绳的学生人数约是；

(4)、现选出了4名跳绳成绩最好的学生，其中有1名男生和3名女生．要从这4名学生中任意抽取2名学生去参加比赛，请用列表法或画树状图法，求刚好抽到1名男生与1名女生的概率．

查看试题解析

身高 $x / cm$	$x < 160$	$160 \leq x < 170$	$170 \leq x < 180$	$x \geq 180$
人数	60	260	550	130

抛掷次数	100	200	300	400	500
正面朝上的频数	53	98	156	202	244

试验次数n	50	100	200	500	1000	2000
相交频数m	23	48	83	207	404	802
相交频率 $\frac{m}{n}$	0.460	0.480	0.415	0.414	0.404	0.401

等级	一般	较好	良好	优秀
阅读量/本	3	4	5	6
频数	12	a	14	4
频率	0.24	0.40	b	c

2023年春季湘教版数学九年级下册第四章 《概率》单元检测A

一、单选题（每题3分，共30分）

二、填空题（每空3分，共18分）

三、解答题（共8题，共72分）

2023年春季湘教版数学九年级下册第四章《概率》单元检测A