2022~2023学年中考数学一轮复习专题07函数图象问题
试卷更新日期:2022-11-25 类型:一轮复习
一、实际应用的图象问题
-
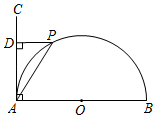
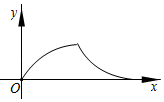
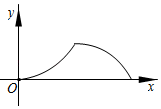
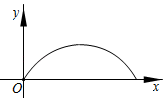
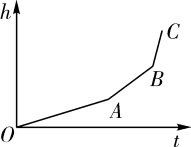
1. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
 A、
A、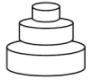 B、
B、 C、
C、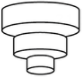 D、
D、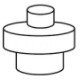 2. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、
2. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、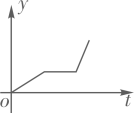 B、
B、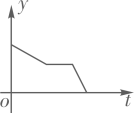 C、
C、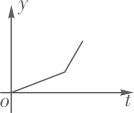 D、
D、 3. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )
3. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )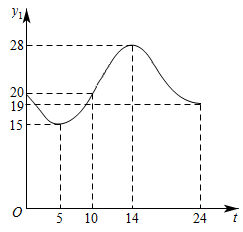 A、
A、 B、
B、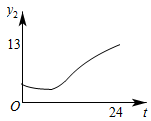 C、
C、 D、
D、 4. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )
4. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )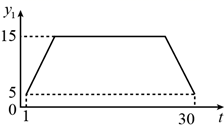 A、
A、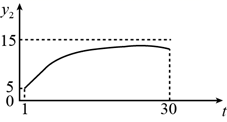 B、
B、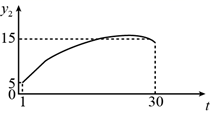 C、
C、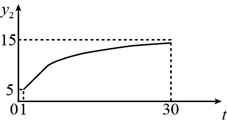 D、
D、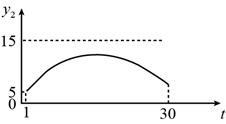 5. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )
5. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )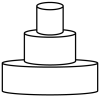 A、
A、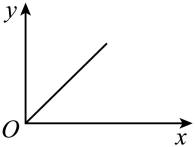 B、
B、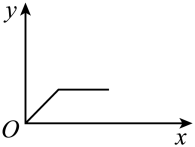 C、
C、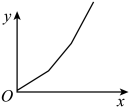 D、
D、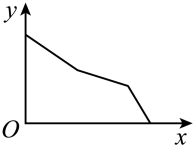 6. 如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( )
6. 如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( ) A、25min~50min,王阿姨步行的路程为800m B、线段CD的函数解析式为 C、5min~20min,王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为
A、25min~50min,王阿姨步行的路程为800m B、线段CD的函数解析式为 C、5min~20min,王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为二、图形平移相关的面积问题
-
7. 如图,等腰与矩形DEFG在同一水平线上, , 现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
 A、
A、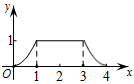 B、
B、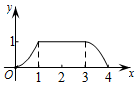 C、
C、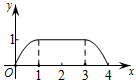 D、
D、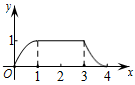 8. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( )
8. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )
9. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )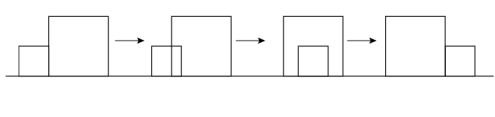 A、
A、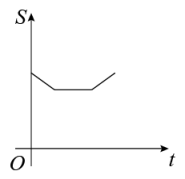 B、
B、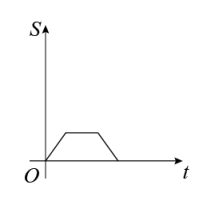 C、
C、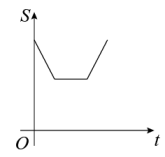 D、
D、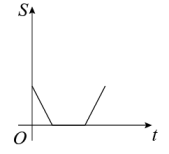 10. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
10. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、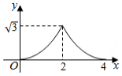 B、
B、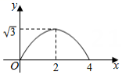 C、
C、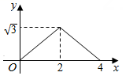 D、
D、
三、单动点面积问题
-
11. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )
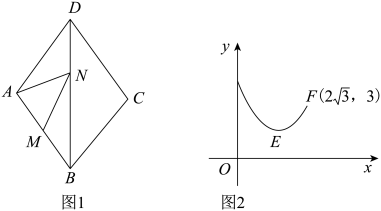 A、 B、 C、 D、12. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
A、 B、 C、 D、12. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )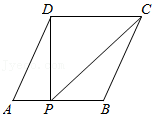 A、
A、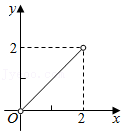 B、
B、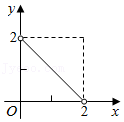 C、
C、 D、
D、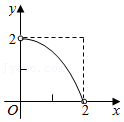 13. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( )
13. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( ) A、
A、 B、
B、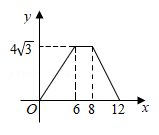 C、
C、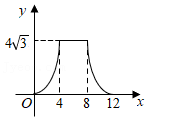 D、
D、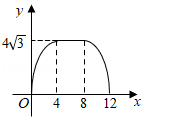 14. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( )
14. 如图①,在正方形ABCD中,点M是AB的中点,点N是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为( ) A、 B、2 C、 D、15. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A、 B、2 C、 D、15. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
四、多动点面积问题
-
16. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
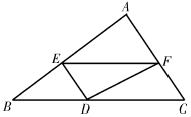 A、
A、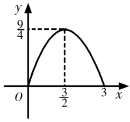 B、
B、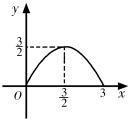 C、
C、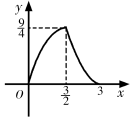 D、
D、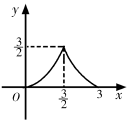 17. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
17. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( ) A、
A、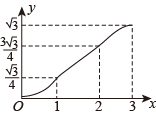 B、
B、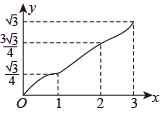 C、
C、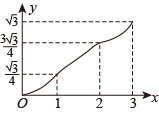 D、
D、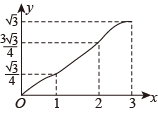 18. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( )
18. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( ) A、
A、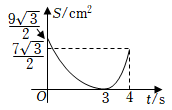 B、
B、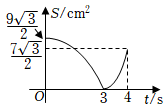 C、
C、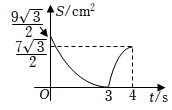 D、
D、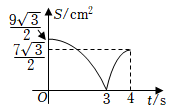 19. 如图,四边形 中, ,垂足分别为E,F,且 , .动点P,Q均以 的速度同时从点A出发,其中点P沿折线 运动到点B停止,点Q沿 运动到点B停止,设运动时间为 , 的面积为 ,则y与t对应关系的图象大致是( )
19. 如图,四边形 中, ,垂足分别为E,F,且 , .动点P,Q均以 的速度同时从点A出发,其中点P沿折线 运动到点B停止,点Q沿 运动到点B停止,设运动时间为 , 的面积为 ,则y与t对应关系的图象大致是( )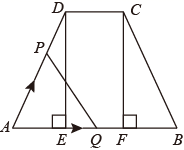 A、
A、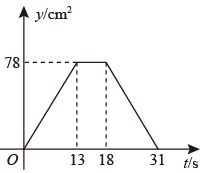 B、
B、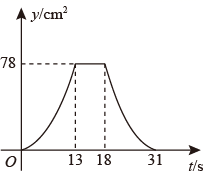 C、
C、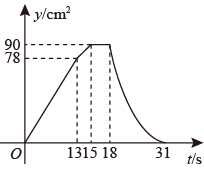 D、
D、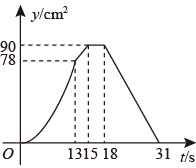
五、四边形相关函数图象问题
-
20. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
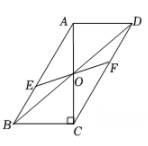 A、
A、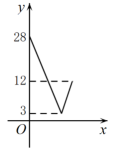 B、
B、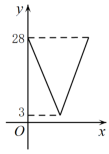 C、
C、 D、
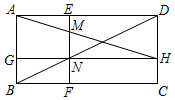
D、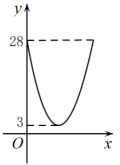 21. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
21. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、