2022~2023学年中考数学一轮复习专题08反比例函数图象问题
试卷更新日期:2022-11-25 类型:一轮复习
一、单种双曲线求K值问题
-
1. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )
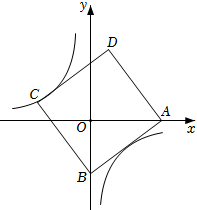 A、4 B、﹣4 C、﹣3 D、32. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、4 B、﹣4 C、﹣3 D、32. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )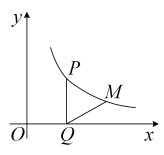 A、 B、 C、 D、43. 如图,点是内一点,与轴平行,与轴平行, , , , 若反比例函数的图象经过 , 两点,则k的值是( )
A、 B、 C、 D、43. 如图,点是内一点,与轴平行,与轴平行, , , , 若反比例函数的图象经过 , 两点,则k的值是( )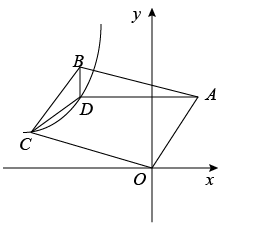 A、 B、-6 C、 D、-124. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A、 B、-6 C、 D、-124. 如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( ) A、8 B、9 C、10 D、115. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )
A、8 B、9 C、10 D、115. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )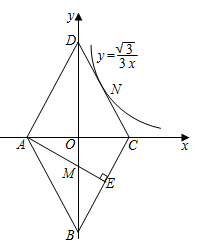 A、 B、 C、 D、6. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )
A、 B、 C、 D、6. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )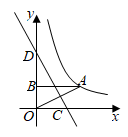 A、 B、 C、 D、7. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )
A、 B、 C、 D、7. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )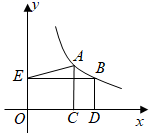 A、2 B、 C、 D、8. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )
A、2 B、 C、 D、8. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )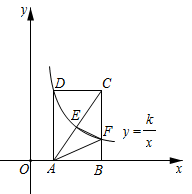 A、 B、 C、2 D、39. 如图,在平面直角坐标系中,菱形 的边 轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数 的图象同时经过顶点 .若点C的横坐标为5, ,则k的值为( )
A、 B、 C、2 D、39. 如图,在平面直角坐标系中,菱形 的边 轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数 的图象同时经过顶点 .若点C的横坐标为5, ,则k的值为( )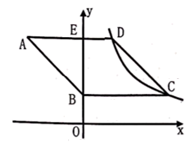 A、 B、 C、 D、10. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )
A、 B、 C、 D、10. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )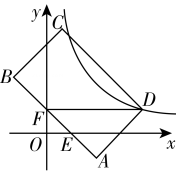 A、 B、3 C、4 D、11. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y= 的图象上,则k的值为( )
A、 B、3 C、4 D、11. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y= 的图象上,则k的值为( ) A、36 B、48 C、49 D、6412. 如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A、36 B、48 C、49 D、6412. 如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )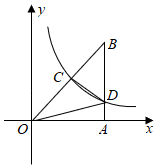 A、3 B、 C、2 D、113. 如图,点A是反比例函数 图象上的一点,过点A作 轴,垂足为点C , D为AC的中点,若 的面积为1,则k的值为( )
A、3 B、 C、2 D、113. 如图,点A是反比例函数 图象上的一点,过点A作 轴,垂足为点C , D为AC的中点,若 的面积为1,则k的值为( )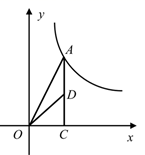 A、 B、 C、3 D、414. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
A、 B、 C、3 D、414. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )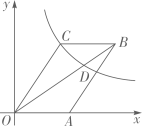 A、 B、 C、 D、15. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )
A、 B、 C、 D、15. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )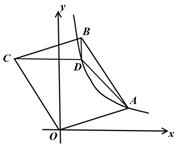 A、 B、4 C、 D、616. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
A、 B、4 C、 D、616. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .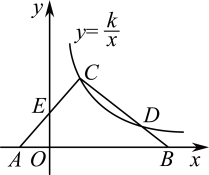 17. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .
17. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .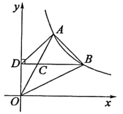 18. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .
18. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .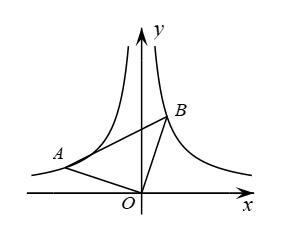 19. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
19. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 . 20. 如图,是边长为10的等边三角形,反比例函数的图象与边、分别交于点A、B(点不与点重合若).于点 , 则的值为.
20. 如图,是边长为10的等边三角形,反比例函数的图象与边、分别交于点A、B(点不与点重合若).于点 , 则的值为.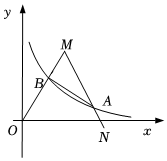 21. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
21. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.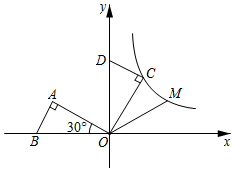
二、两种双曲线求K值问题
-
22. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
 A、3 B、-3 C、 D、23. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
A、3 B、-3 C、 D、23. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )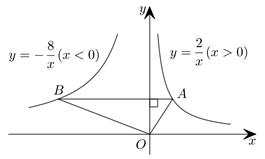 A、3 B、5 C、6 D、1024. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A、3 B、5 C、6 D、1024. 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )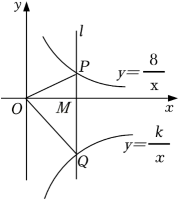 A、38 B、22 C、﹣7 D、﹣2225. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )
A、38 B、22 C、﹣7 D、﹣2225. 如图,正方形 的顶点分别在反比例函数 和 的图象上.若 轴,点 的横坐标为3,则 ( )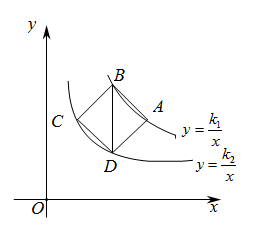 A、36 B、18 C、12 D、926. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )
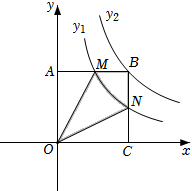
A、36 B、18 C、12 D、926. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )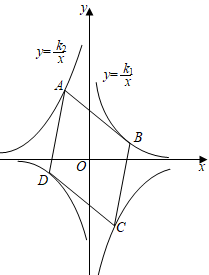 A、 B、 C、 D、27. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A、 B、 C、 D、27. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )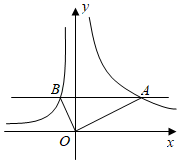 A、5t B、 C、 D、528. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、5t B、 C、 D、528. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )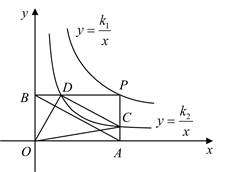 A、①② B、①③ C、②③ D、①29. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A、①② B、①③ C、②③ D、①29. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )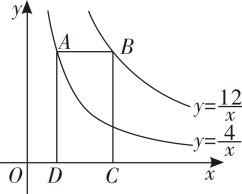 A、4 B、6 C、8 D、1230. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )
A、4 B、6 C、8 D、1230. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )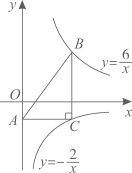 A、3 B、4 C、5 D、631. 如图所示,过y轴正半轴上的任意一点P , 作x轴的平行线,分别与反比例函数 和 的图象交于点A和点B , 若点C是x轴上任意一点,连接 ,则 的面积为( )
A、3 B、4 C、5 D、631. 如图所示,过y轴正半轴上的任意一点P , 作x轴的平行线,分别与反比例函数 和 的图象交于点A和点B , 若点C是x轴上任意一点,连接 ,则 的面积为( )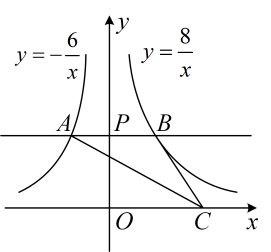 A、6 B、7 C、8 D、1432. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( )
A、6 B、7 C、8 D、1432. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.P为y轴上一点,连接 , .则 的面积为( ) A、5 B、6 C、11 D、1233. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= .
A、5 B、6 C、11 D、1233. 如图,四边形OABC是平行四边形,点O是坐标原点,点C在y轴上,点B在反比例函数y=(x>0)的图象上,点A在反比例函数y=(x>0)的图象上,若平行四边形OABC的面积是7,则k= . 34. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
34. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .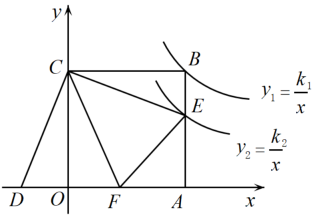 35. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= .
35. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= . 36. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
36. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .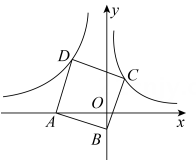 37. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
37. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.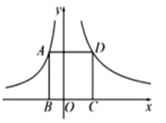
三、函数图象共存问题
-
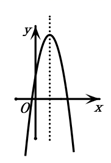
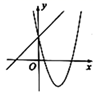
38. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
 A、
A、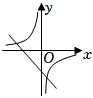 B、
B、 C、
C、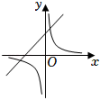 D、
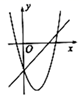
D、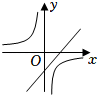 39. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
39. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、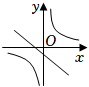 B、
B、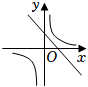 C、
C、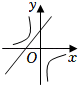 D、
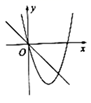
D、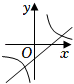 40. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
40. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )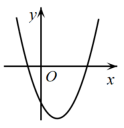 A、
A、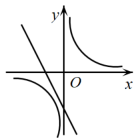 B、
B、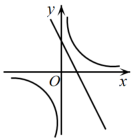 C、
C、 D、
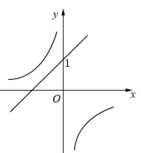
D、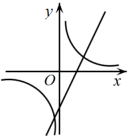 41. 已知一次函数 的图象如图所示,则 与 的图象为( )
41. 已知一次函数 的图象如图所示,则 与 的图象为( )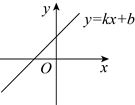 A、
A、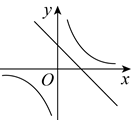 B、
B、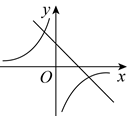 C、
C、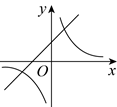 D、
D、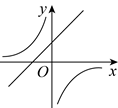 42. 已知反比例函数 的图象如图所示,则一次函数 和二次函数 在同一平面直角坐标系中的图象可能是( )
42. 已知反比例函数 的图象如图所示,则一次函数 和二次函数 在同一平面直角坐标系中的图象可能是( )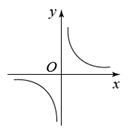 A、
A、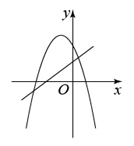 B、
B、 C、
C、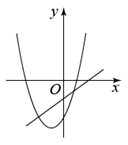 D、
D、