安徽省宣城六校2022-2023学年高二上学期数学期中联考试卷
试卷更新日期:2022-11-25 类型:期中考试
一、单选题
-
1. 已知命题p: , , 则命题p的否定是( )A、 , B、 , C、 , D、 ,2. 已知集合 , 则以下关系正确的是( )A、 B、 C、 D、3. 函数的定义域是( )A、 B、 C、 D、4. 已知幂函数的图象过点 , 则的值为( )A、3 B、9 C、27 D、5. 对于任意实数 ,以下四个命题中的真命题是( )A、若 , , 则 B、若 , , 则 C、若 , 则 D、若 , 则6. 函数 的图象大致为( )A、
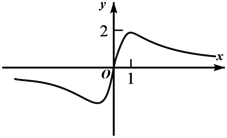 B、
B、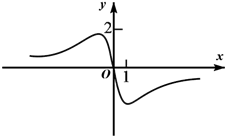 C、
C、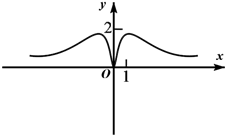 D、
D、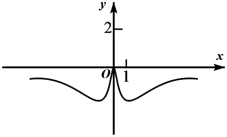 7. 已知某商品的进货成本为10(元/件),经过长时间调研,发现售价x(元)与月销售量y(件)满足函数关系式 .为了获得最大利润,商品售价应为( )A、80元 B、60元 C、50元 D、40元8. 若正数满足 , 则的最小值为( )A、6 B、 C、 D、9. 已知:是集合到集合的函数,如果集合 , 那么集合可能为( )A、 B、{-2} C、 D、{2}
7. 已知某商品的进货成本为10(元/件),经过长时间调研,发现售价x(元)与月销售量y(件)满足函数关系式 .为了获得最大利润,商品售价应为( )A、80元 B、60元 C、50元 D、40元8. 若正数满足 , 则的最小值为( )A、6 B、 C、 D、9. 已知:是集合到集合的函数,如果集合 , 那么集合可能为( )A、 B、{-2} C、 D、{2}二、多选题
-
10. 下列式子中,可以是的必要条件的有( )A、 B、 C、 D、11. 若不等式的解集为R,则实数a的取值可以是( )A、-10 B、-8 C、0 D、212. 德国著名数学家狄利克雷在数学领域成就显著,是解析数论的创始人之一,以其名命名的函数 成为狄利克雷函数,则关于 ,下列说法正确的是( )A、 B、 C、函数 是偶函数 D、 有2个实数根
三、填空题
-
13. 若 , 集合A={1,a,a+2},B={1,3,5},且A=B,则a=.14. 若直角三角形斜边长等于cm,则直角三角形面积的最大值为.15. 已知函数 , 则.
四、解答题
-
16. 已知命题p: , , q: , 若p的否定是假命题,且q是真命题,求实数a的取值范围.17. 设集合 , , .(1)、求;(2)、求.18. 已知函数是定义在上的奇函数,且.(1)、求的值;(2)、判断在上的单调性,并用定义证明;19. 已知函数 为幂函数,且在区间 上单调递减.(1)、求实数 的值;(2)、请画出函数 的草图.
