四川省绵阳市2022-2023学年高一上学期数学期中考试试卷

试卷更新日期：2022-11-25 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in Z | - 2 < x < 1}$ ，则下列选项正确的是（）

A、 $- 2 \in A$ B、 $0 \subseteq A$ C、 $1 \notin A$ D、 ${1} \subseteq A$

查看试题解析
2. 下列命题中正确的是（）

A、存在 $x \in Z$ ，使得x同时被2和3整除 B、有的三角形没有外接圆 C、幂函数 $y = x^{\frac{2}{3}}$ 在 $(0 ， + \infty)$ 内是减函数 D、任何实数都有算术平方根

查看试题解析
3. 若 $a > b > 0$ ，则下列选项错误的是（）

A、 $\frac{1}{a} < \frac{1}{b}$ B、 $2^{a} > 2^{b}$ C、 $a c^{2} > b c^{2}$ D、 $a^{2} > b^{2}$

查看试题解析
4. 全称量词命题：“ $\forall x > 1 ， x^{2} > 1$ .”的否定为（）

A、 $\forall x > 1 ， x^{2} < 1$ B、 $\forall x \leq 1 ， x^{2} \leq 1$ C、 $\exists x \leq 1 ， x^{2} \leq 1$ D、 $\exists x > 1 ， x^{2} \leq 1$

查看试题解析
5. 下列选项中，在定义域内既是奇函数又是增函数的为（）

A、 $y = - x^{3}$ B、 $y = \frac{1}{x}$ C、 $y = | x |$ D、 $y = x | x |$

查看试题解析
6. 若函数 $f (x) = x^{2} + b x + c$ 在区间 $(2 ， + \infty)$ 上是单调函数，则实数b的取值范围是（）

A、 $(- 4 ， + \infty)$ B、 $[- 4 ， + \infty)$ C、 $(- \infty ， - 4]$ D、 $(- \infty ， - 4)$

查看试题解析
7. 如图，函数 $f (x) = \frac{m_{1} x + 1}{x + 1} (x \geq 0)$ 与 $g (x) = \frac{m_{2} x + 1}{x + 1} (x \geq 0)$ 的部分图象分别为 $C_{1} ， C_{2}$ ，则正确的是（）

A、 $0 < m_{2} < m_{1} < 1$ B、 $m_{1} > 1 > m_{2} > 0$ C、 $0 < m_{1} < 1 ， m_{2} < - 1$ D、 $m_{1} > 1 ， m_{2} < - 1$

查看试题解析
8. 三个数 $a = {(\frac{3}{2})}^{\frac{3}{4}} ， b = {(\frac{3}{4})}^{\frac{3}{2}} ， c = {(\sqrt{2})}^{- \frac{3}{2}}$ 之间的大小关系是（）

A、 $a < c < b$ B、 $a < b < c$ C、 $c < b < a$ D、 $b < c < a$

查看试题解析

二、多选题

9. 下列选项中，满足p是q的充分条件的是（）

A、 $p ： x > \sqrt{2} ， q ： x > 1$ B、 $p ： m = 0 ， q ： m n = 0$ C、 $p ： x^{2} \neq 0 ， q ： x \neq 0$ D、 $p ： x > y ， q ： x^{2} > y^{2}$

查看试题解析
10. 设m，n是方程 $2 x^{2} + 3 x - 1 = 0$ 的两根，则下面各式值等于8的有（）

A、 $m^{2} + n^{2}$ B、 ${(\frac{1}{4})}^{m + n}$ C、 ${(64)}^{m n}$ D、 ${(\frac{1}{6 4^{m}})}^{n}$

查看试题解析
11. 某外贸公司在30天内A商品的销售价格P（元）与时间t（天）的关系满足下方图象所示的函数，A商品的销售量Q（万件）与时间t（天）的关系为 $Q = 40 - t$ ，则下列说法正确的是（）

A、第15天的销售额最大 B、第20天的销售额最大 C、最大销售额为125万元 D、最大销售额为120万元

查看试题解析
12. 定义在R上的函数 $f (x)$ ，对任意的 $x_{1} ， x_{2} \in R$ ，都有 $f (x_{1} + x_{2}) = f (x_{1}) + f (x_{2}) + 1$ ，且当 $x > 0$ 时， $f (x) > f (0)$ 恒成立，下列说法正确的是（）

A、 $f (0) = - 1$ B、函数 $f (x)$ 的单调增区间为 $(0 ， + ∞)$ C、函数 $g (x) = f (x) + 1$ 为奇函数 D、函数 $f (x)$ 为R上的增函数

查看试题解析

三、填空题

13. 已知集合 $A = {x | | x | < 2}$ ， $B = {x | - 2 \leq x \leq 1}$ ，则 $A ∩ B =$ .

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} 3^{x} - (\frac{1}{3})^{x} ， x < 0 \\ 2 x - 2 ， x \geq 0 \end{array}$ ，则 $f (f (\frac{1}{2})) =$ ．

查看试题解析
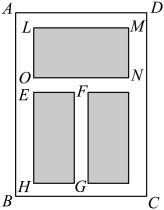
15. 若奇函数 $f (x)$ 在 $(a ， b]$ 上的值域为 $[- \sqrt{2} ， 2)$ ，则该函数在区间 $[- b ， - a)$ 上的值域为．

查看试题解析
16. 某学校计划在运动场内规划面积为 $1600 m^{2}$ 的矩形区域ABCD用于全校师生核酸检测.矩形区域内布置成如右图所示的三个检测点（阴影部分）.已知下方是两个相同的矩形检查点，每个检测点区域四周各留下 $1 m$ 宽的间隔，若上方矩形宽LO是下方矩形边长EH的一半，为使三个检测点面积之和达到最大值，则 $A B =$ m.

查看试题解析

四、解答题

17. 已知集合 $A = {x | 4 - m \leq x \leq 4 + m} ， B = {x | x^{2} - 6 x \geq 0}$ .

(1)、当 $m = 3$ 时，求 $∁_{R} B ， A ∪ B$ ；

(2)、若 $m > 0$ ，且 $A$ 是 $∁_{R} B$ 的真子集，求实数m的取值范围.

查看试题解析
18. 《几何原本》卷2的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，利用这一方法，很多代数的公理或定理都能够通过图形实现证明．现有如图所示图形，点F在半圆O上，且 $O F ⊥ A B$ ，点C在线段OB上．设 $A C = a$ ， $B C = b$ ．结合该图形解答以下问题：

(1)、用a，b表示OF，OC，FC；

(2)、根据OF与FC的大小关系，结合（1）的结论可得到什么不等式？并证明 $a = b$ 是该不等式取等号的充要条件．

查看试题解析
19. 已知幂函数 $f (x) = (m^{2} - 6 m + 10) x^{- n^{2} + 4 n} (n > 1 ， n \in Z ， m \in R)$ 的图象关于y轴对称，且在 $(0 ， + ∞)$ 上单调递增.

(1)、求m和n的值；

(2)、求满足不等式 ${(2 a + 3)}^{- \frac{m}{3}} < {(a - 1)}^{- \frac{n}{2}}$ 的a的取值范围.

查看试题解析
20. 已知关于x的不等式 $a x^{2} + 3 x + 2 > 0$ 的解集为 ${x | x < b$ 或 $x > - 1} (b < - 1)$ .

(1)、求实数a，b的值；

(2)、当 $x \in [1 ， 3]$ 时，求函数 $f (x) = \frac{a x^{2} + 3 x + 2}{x}$ 的值域.

查看试题解析
21. 某工厂生产某种产品，年固定成本为300万元，可变成本 $q (x)$ （万元）与年产量x（件）的关系为 $q (x) = {\begin{array}{l} \frac{1}{3} x^{2} + 10 x ， 0 < x < 80 \\ \frac{51 x^{2} - 2020 x + 25100}{x - 10} ， x \geq 80 \end{array}$ ，每件产品的售价为50万元，且工厂每年生产的产品都能全部售完.

(1)、将年盈利额W（万元）表示为年产量x（件）的函数；

(2)、求年盈利额的最大值及相应的年产量.

查看试题解析
22. 设函数 $f (x) = a^{x} - a^{- x}$ （ $x \in R ， a > 0$ ，且 $a \neq 1$ ）.

(1)、若 $a > 1$ ，用定义证明 $f (x)$ 为 $R$ 上的增函数；

(2)、已知 $f (1) = \frac{3}{2}$ ，函数 $g (x) = a^{2 x} + a^{- 2 x} - 2 m f (x)$ ，若函数 $g (x)$ 在 $[1 ， + \infty)$ 上的最小值为 $- 7$ ，求实数m的值.

查看试题解析