内蒙古自治区呼和浩特市2022-2023学年高一上学期数学期中考试试题
试卷更新日期:2022-11-25 类型:期中考试
一、单选题
-
1. 下列关系中,正确的是( )A、 B、 C、 D、2. 已知集合 , ,若 ,则所有实数m组成的集合是( )A、 B、 0, C、 D、 0,3. 若a,b,c为实数,且 , 则下列命题正确的是( )A、 B、 C、 D、4. 已知集合 , , 则( )A、 B、 C、 D、5. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,6. 若 则一定有( )A、 B、 C、 D、7. 如果 ,那么下列不等式中正确的是( )A、 B、 C、 D、8. 已知 , , 则下列不等式恒成立的是( )A、 B、 C、 D、9. 已知x<-2,y>4,则的取值范围是( )A、 B、 C、 D、10. 集合 , 用列举法可以表示为( )A、 B、 C、 D、11. 集合A={1,2,4},B={x|x2∈A},将集合A、B分别用如图中的两个圆表示,则圆中阴影部分表示的集合中元素个数恰好为4的是( )A、
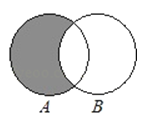 B、
B、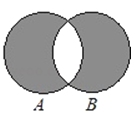 C、
C、 D、
D、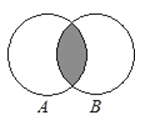 12. 非空集合P满足下列两个条件:(1) , (2)若元素 , 则 , 则集合P个数是( )A、4 B、5 C、6 D、7
12. 非空集合P满足下列两个条件:(1) , (2)若元素 , 则 , 则集合P个数是( )A、4 B、5 C、6 D、7二、填空题
-
13. 命题“存在x∈R,使得x2+2x+5=0”的否定是14. 已知实数满足 , 则的取值范围是.15. 写出下列不等式的解集,:;: .
三、解答题
-
16. 设集合 . 求:(1)、;(2)、;(3)、17.(1)、若或 , 则 . 写出其逆命题、否命题、逆否命题,并分别指出真假;(2)、设原命题是:当c>0时,若a>b,则ac>bc,写出其逆命题、否命题、逆否命题,并分别指出真假.18.(1)、已知 , , 求 , 取值范围;(2)、已知 , , 求的取值范围.