湖北省部分省级示范高中2022-2023学年高一上学期数学期中联考试卷

试卷更新日期：2022-11-25 类型：期中考试

进入出卷网下载

一、单选题

1. 命题“ $\forall x \in R, x^{2} - 2 x + 1 \geq 0$ ”的否定是（）

A、 $\exists x \in R, x^{2} - 2 x + 1 \leq 0$ B、 $\exists x \in R, x^{2} - 2 x + 1 \geq 0$ C、 $\exists x \in R, x^{2} - 2 x + 1 < 0$ D、 $\forall x \in R, x^{2} - 2 x + 1 < 0$

查看试题解析
2. 幂函数 $f (x) = (m^{2} - 6 m + 9) x^{m^{2} - 3 m + 1}$ 在 $(0 ， + \infty)$ 上单调递增，则 $m$ 的值为（）

A、2 B、3 C、4 D、2或4

查看试题解析
3. 已知全集为 $R$ ，集合 $A = {- 1, 0, 1, 2, 3}$ ， $B = {x | \frac{x - 2}{x + 1} \geq 0}$ ，则 $A \cap B$ 元素个数为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 函数 $f (x) = \frac{4}{x - 3} + x (x < 3)$ 的最大值是（）

A、-4 B、1 C、5 D、-1

查看试题解析
5. 不等式 $2 x^{2} - 5 x - 3 < 0$ 的一个必要不充分条件是（）

A、 $- 3 < x < \frac{1}{2}$ B、 $- 1 < x < 6$ C、 $- \frac{1}{2} < x < 0$ D、 $\frac{1}{2} < x < 3$

查看试题解析
6. 函数 $f (x) = a x^{2} + 2 x - 1 ，$ 在 $[1 ， 2]$ 上是增函数，则 $a$ 的取值范围是（）

A、 $[- \frac{1}{2} ， 0]$ B、 $[- \frac{1}{2} ， \infty)$ C、 $[- \frac{1}{2} ， 0) ∪ (0 ， + \infty)$ D、 $(0 ， + \infty)$

查看试题解析
7. 若不等式 $a x^{2} + b x + c > 0$ 的解集为 ${x | - 1 < x < 2}$ ，那么不等式 $a (x^{2} + 1) + b (x - 1) + c > 2 a x$ 的解集为（）

A、 ${x | - 2 < x < 1}$ B、 ${x | x < - 2 或 x > 1}$ C、 ${x | x < 0 或 x > 3}$ D、 ${x | 0 < x < 3}$

查看试题解析
8. 已知函数 $f (x) = {\begin{array}{l} - x^{2} + a x ， x ⩽ 2 \\ 2 a x - 5 ， x > 2 \end{array}$ ，若存在 $x_{1}$ ， $x_{2} \in R$ ，且 $x_{1} \neq x_{2}$ ，使得 $f (x_{1}) = f (x_{2})$ ，则实数 $a$ 的取值范围为 $($ $)$

A、 $(- \infty ， 4)$ B、 $(- \infty ， \frac{1}{4})$ C、 $(- \infty ， 3)$ D、 $(- \infty ， 8)$

查看试题解析

二、多选题

9. 图中阴影部分用集合符号可以表示为（）

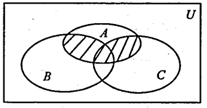A、 $A \cap (B \cup C)$ B、 $A \cup (B \cap C)$ C、 $A \cap ∁_{U} (B \cap C)$ D、 $(A \cap B) \cup (A \cap C)$

查看试题解析
10. 有以下判断，其中是正确判断的有（）

A、 $f (x) = \frac{| x |}{x}$ 与 $g (x) = {\begin{array}{l} 1 ， x \geq 0 \\ - 1 ， x < 0 \end{array}$ 表示同一函数； B、函数 $y = f (x)$ 的图象与直线 $x = 1$ 的交点最多有 1 个 C、函数 $f (x) = x^{2} + 2 + \frac{1}{x^{2} + 2}$ 的最小值为 2 D、若 $f (x) = | x - 1 | - | x |$ ，则 $f (f (\frac{1}{2})) = 1$

查看试题解析
11. 《几何原本》中的几何代数法（用几何方法研究代数问题）成了后世西方数学家处理问题的重要依据根据这一方法，很多代数公理、定理都能够通过图形实现证明，并称之为“无字证明”如图所示，AB是半圆O的直径，点C是AB上一点（不同于A，B， $O$ ），点D在半圆O上，且 $C D ⊥ A B$ ， $C E ⊥ O D$ 于点 $E .$ 设 $| A C | = a$ ， $| B C | = b$ ，则该图形可以完成的“无字证明”为（）

A、 $\sqrt{a b} < \frac{a + b}{2} (a > 0 ， b > 0 ， a \neq b)$ B、 $\frac{a + b}{2} < \frac{2 a b}{a + b} (a > 0 ， b > 0 ， a \neq b)$ C、 $\frac{2 a b}{a + b} < \sqrt{a b} (a > 0 ， b > 0 ， a \neq b)$ D、 $\sqrt{\frac{a^{2} + b^{2}}{2}} > \frac{a + b}{2} (a > 0 ， b > 0 ， a \neq b)$

查看试题解析
12. 函数 $y = f (x)$ 图像关于坐标原点成中心对称图形的充要条件是函数 $y = f (x)$ 为奇函数，有同学据此推出以下结论，其中正确的是（）

A、函数 $y = f (x)$ 的图像关于点 $P (a ， b)$ 成中心对称的图形的充要条件是 $y = f (x + a) - b$ 为奇函数 B、函数 $f (x) = x^{3} - 3 x^{2}$ 的图像的对称中心为 $(1 ， - 2)$ C、函数 $y = f (x)$ 的图像关于 $x = a$ 成轴对称的充要条件是函数 $y = f (x - a)$ 是偶函数 D、函数 $g (x) = | x^{3} - 3 x^{2} + 2 |$ 的图像关于直线 $x = 1$ 对称

查看试题解析

三、填空题

13. 已知函数 $f (x) = a x^{5} - b x^{3} + c x - 3$ ， $f (- 3) = 7$ ，则 $f (3)$ 的值为.

查看试题解析
14. 已知集合A＝{x|x＜－1或x≥1}，B＝{x|2a＜x≤a＋1，a＜1}，B⊆A，则实数a的取值范围为．

查看试题解析
15. 若对任意 $x \geq 0$ ， $k \sqrt{1 + x} ⩾ 1 + \sqrt{x}$ 恒成立，则实数 $k$ 的取值范围是.

查看试题解析
16. 设 $f (x) = {\begin{array}{l} {(x - a)}^{2} ， x \leq 0 \\ x + \frac{1}{x} ， x ＞ 0 \end{array}$ ．当 $a = \frac{1}{2}$ 时，f（x）的最小值是；若f（0）是f（x）的最小值，则a的取值范围是．

查看试题解析

四、解答题

17. 已知集合 $A = {x ∣ 0 < 2 x + a \leq 3} ， B = {y ∣ - \frac{1}{2} < y < 2}$

(1)、当 $a = 1$ 时，求 $(∁_{U} B) \cup A$ ；

(2)、若 $A \subseteq B$ ，求a的取值范围

查看试题解析
18. 已知点 $(\sqrt{2} ， 2)$ 在幂函数 $f (x)$ 的图像上.

(1)、求 $f (x)$ 的解析式；

(2)、若函数 $g (x) = f (x) + a x + 3$ ， $x \in [1 ， + ∞)$ 是否存在实数a，使得 $g (x)$ 最小值为5？若存在，求出a的值；若不存在，说明理由

查看试题解析
19. 为响应国家提出的“大众创业，万众创新”的号召，小李同学大学毕业后，决定利用所学专业进行自主创业．经过调查，生产某小型电子产品需投入年固定成本5万元，每年生产x万件，需另投入流动成本C(x)万元，且C(x)＝ ${\begin{array}{l} \frac{1}{2} x^{2} + 4 x ， 0 < x < 8 \\ 11 x + \frac{49}{x} - 35 ， x \geq 8 \end{array}$ 每件产品售价为10元，经分析，生产的产品当年能全部售完．

(1)、写出年利润P(x)(万元)关于年产量x(万件)的函数解析式(年利润＝年销售收入－固定成本－流动成本)．

(2)、年产量为多少万件时，小李在这一产品的生产中所获利润最大？最大利润是多少？

查看试题解析
20. 已知a，b均为正数，且满足 $a + b + 8 = a b$ ．

(1)、求 $a b$ 的最小值及取到最小值时a与b的值；

(2)、求 $\frac{(a b - 8) (a + 4 b)}{a b}$ 的最小值及取到最小值时a与b的值．

查看试题解析
21. 设函数 $f (x) = a x^{2} + (b - 2) x + 3$ .

(1)、当 $f (1) = 3$ ，且 $a > 0$ 时，解关于x的不等式 $f (x) > 0$ ；

(2)、当 $f (1) = 2$ ，若“ $- 1 < x < 1$ ”是“ $f (x) > 2$ ”成立的充分条件，求实数a的取值范围.

查看试题解析
22. 已知函数 $f (x) = | x - a | - \frac{9}{x} + a$ ， a∈R.

(1)、若a=0，试判断f(x)的奇偶性，并说明理由；

(2)、若函数 $f (x)$ 在[1，a]上单调，且对任意x∈[1，a]， $f (x)$ <-2恒成立，求a的取值范围；

(3)、若x∈[1，6]，当a∈(3，6)时，求函数 $f (x)$ 的最大值的表达式M(a).

查看试题解析