2022-2023学年冀教版数学七年级上册期末模拟试卷1

试卷更新日期：2022-11-25 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共36分）

1. 下列各组数中，互为相反数的是（）

A、4与 $\frac{1}{4}$ B、 ${(- 2)}^{2}$ 与 $| - 4 |$ C、 $- (- 4)$ 与 $- 2^{2}$ D、 $- 4$ 与 $- | - 4 |$

查看试题解析
2. 在 $\frac{3}{5} ， - \frac{1}{2} ， + 3.5 ， 0 ， - \frac{π}{2} ， - 0.7$ 中，其中有理数的个数有（）

A、3 个 B、4 个 C、5 个 D、6 个

查看试题解析
3. 如图，从点O出发的5条射线，可以组成的锐角的个数是（）

A、8 B、9 C、10 D、11

查看试题解析
4. 一个两位数，个位上的数字是a，十位上的数字是b，用代数式表示这个两位数是（）

A、ab B、ba C、10a+b D、10b+a

查看试题解析
5. 下列说法正确的是（）

A、单项式a的次数是0 B、 $\frac{1}{x} + 1$ 是一次多项式 C、多项式 $a^{4} + 2 a b^{2} + 3$ 的次数是3次 D、 $2^{3}$ 和 $3^{2}$ 是同类项

查看试题解析
6. 按图示的程序计算，若开始输入的x为正整数，最后输出的结果为67，则x的值是（　）

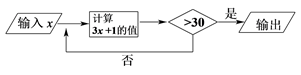A、2或7 B、2或22 C、2或22或7 D、2或12或22

查看试题解析
7. 如图，已知B，C两点把线段AD从左至右依次分成2：4：3三部分，M是AD的中点，BM＝5cm，则线段MC的长为（）

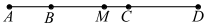A、1cm B、2cm C、3cm D、4cm

查看试题解析
8. 已知关于x的方程2x+a=1-x与方程2x-3=1的解相同，则a的值为（）

A、2 B、-2 C、5 D、-5

查看试题解析
9. 若 $3 x^{n + 5} y$ 与 $- x^{4} y$ 是同类项，则n的值为（）

A、1 B、 $- 4$ C、 $- 1$ D、4

查看试题解析
10. 如图，BD在∠ABC的内部，∠ABD＝ $\frac{1}{3}$ ∠CBD，如果∠ABC＝80°，则∠ABD＝（）

A、 $(\frac{80}{3})^{°}$ B、20° C、60° D、 $(\frac{160}{3})^{°}$

查看试题解析
11. 如图所示：把两个正方形放置在周长为 $m$ 的长方形 $A B C D$ 内，两个正方形的重叠部分的周长为 $n$ (图中阴影部分所示)，则这两个正方形的周长和可用代数式表示为（）

A、 $m + n$ B、 $m - n$ C、 $2 m - n$ D、 $m + 2 n$

查看试题解析
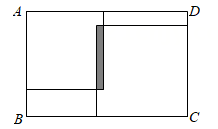12. 如图，C为射线AB上一点，AB＝30，AC比BC的 $\frac{1}{4}$ 多5，P，Q两点分别从A，B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：①BC＝2AC；②AB＝4NQ；③当PB＝ $\frac{1}{2}$ BQ时，t＝12，其中正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（每空3分，共18分）

13. 一个角为 $24 ° 40^{'}$ ，则它的余角度数为．

查看试题解析
14. 1米长的小棒，第1次截去 $\frac{1}{2}$ ，第2次截去剩下的 $\frac{1}{2} ，$ 如此截下去，第五次后剩下的小棒的长度为．

查看试题解析
15. $a$ 、 $b$ 、 $c$ 在数轴上的位置如图所示：试化简 $| a - b | - 2 c - | c + b | + | 3 b | =$ .

查看试题解析
16. 已知a、b为常数，且三个单项式2xy²、axy^3-b、-xy相加得到的和仍为单项式，则a+b的值为．

查看试题解析
17. 某种商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为 .

查看试题解析
18. 规定一种运算“*”，a*b= $\frac{1}{3}$ a﹣ $\frac{1}{4}$ b，则方程x*2=1*x的解为．

查看试题解析

三、解答题（共7题，共66分）

19. 计算：

(1)、 $\frac{1}{3} - \frac{3}{4} - (- 4 \frac{2}{3}) + (- 2 \frac{1}{4}) - | - 2 |$

(2)、 $(\frac{7}{4} - \frac{7}{8} - \frac{7}{12}) \div (- \frac{7}{8}) + (- \frac{8}{3})$

(3)、 $- 3^{3} \div 3 + (- 2 - 5)^{2} - (- \frac{4}{9}) \times (- 3)^{2}$

查看试题解析
20. 解方程

(1)、 $3 (x - 2) + 5 = 0$

(2)、 $\frac{y - 3}{2} - 1 = \frac{2 y + 1}{3}$

查看试题解析
21. 先化简，再求值： $4 (x^{2} y + \frac{1}{2} x y^{2}) - 3 (x^{2} y - x) - 2 x y^{2} + 1$ ，其中x＝-2，y＝3．

查看试题解析

22. 为鼓励居民节约用电，某省试行阶段电价收费制，具体执行方案如表：

档次	每户每月用电量（度）	执行电价（元/度）
第一档	小于等于200	0.55
第二档	大于200小于400	0.6
第三档	大于等于400	0.85

某户居民五、六月份共用电500度，缴电费290.5元.已知该用户六月份用电量大于五月份，且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度？

查看试题解析

23. 学校为开展“课后延时服务”，计划购买一批乒乓球拍和羽毛球拍，已知一副羽毛球拍的单价比乒乓球拍贵20元，购买12副乒乓球拍和8副羽毛球拍共1360元．

(1)、每副乒乓球拍和羽毛球拍的单价各是多少元？

(2)、在“双11”促销活动中，某商店制定以下优惠方案：
方案一：商品按原价打9折优惠；

方案二：商品按原价购买，超过2000元的部分打7折优惠；

现计划购买30副乒乓球拍和20副羽毛球拍，请通过计算说明按照那种方案购买较为合算？

查看试题解析
24. 如图，将一副直角三角板的直角顶点C叠放在一起.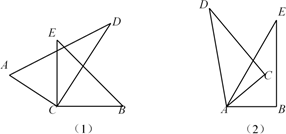

(1)、如图（1），若∠DCE＝33°，则∠BCD＝， ∠ACB＝.

(2)、如图（1），猜想∠ACB与∠DCE的大小有何特殊关系？并说明理由.

(3)、如图（2），若是两个同样的直角三角板60°锐角的顶点A重合在一起，则∠DAB与∠CAE的数量关系为.

查看试题解析
25. 已知数轴上有A、B、C三个点，分别表示有理数 $- 24$ ， $- 10$ ， 10，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．

(1)、用含t的代数式表示P到点A和点C的距离：PA= ， PC= ．

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A，则点P出发17秒后 $Q A$ = ， $P Q$ = ．

(3)、在点Q开始运动后， P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．

查看试题解析