2023年春季湘教版数学九年级下册第三章 《投影与视图》单元检测B
试卷更新日期：2022-11-24 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 如图为一个几何体的表面展开图，则该几何体是（ ）
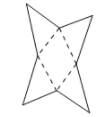A、三棱锥 B、四棱锥 C、四棱柱 D、圆锥2. 泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的（ ）
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似3. 如图是正方体的表面展开图，每个面内都分别写有一个字，则与“创”字相对面上的字是（ ）
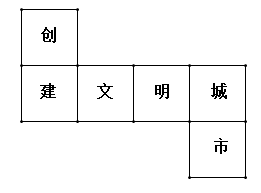A、文 B、明 C、城 D、市4. 如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是（ ）
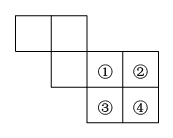A、① B、② C、③ D、④5. 如图1所示，将长为6的矩形纸片沿虚线折成3个矩形，其中左右两侧矩形的宽相等，若要将其围成如图2所示的三棱柱形物体，则图中a的值可以是（ ）
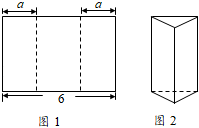A、1 B、2 C、3 D、46. 如图，是一个正方体截去一个角后得到的几何体，则该几何体的左视图是（ ）
A、
B、
C、
D、
7. 如图所示是一个由若干个相同的正方体组成的几何体的主视图和左视图，则组成这个几何体的小正方体的个数最少是（ ）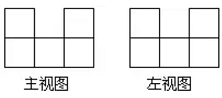
A、5个 B、6个 C、11个 D、13个8. 如图，这个几何体是由5个相同的小立方块搭成的，若移走一个小立方块，从左面看到几何体的形状发生了改变，则移走的小立方块是（ ）
A、① B、② C、③ D、④9. 圆桌面（桌面中间有一个直径为1m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为2m，桌面离地面1m，若灯泡离地面2m，则地面圆环形阴影的面积是（ ）
A、2πm2 B、3πm2 C、6πm2 D、12πm210. 如图，一个正六棱柱的表面展开后正好放入一个矩形内，把其中一部分图形挪动了位置，发现矩形的长留出 ，宽留出 ，则该六棱柱的侧面积是（ ）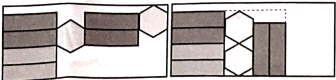
A、 B、 C、 D、二、填空题（每空3分，共18分）
-
11. 一个正方体盒子的展开图如图所示，如果要把它粘成一个正方体，那么与点A重合的点是点.
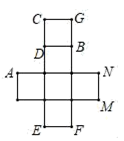12. 如图是一个正方体的展开图，正方体相对面的数字或代数式互为相反数，则x的值为 ， y的值为 ．
13. 如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方，某一时刻，太阳光线恰好垂直照射叶片、 ， 此时各叶片影子在点M右侧成线段 ． 测得 ， ， 垂直于地面的木棒与影子的比为 ． 则点O、M之间的距离等于m；
14. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积是 ．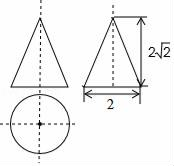
15. 老师用10个1cm×1cm×1cm的小正方体摆出一个立体图形，它的主视图如图①所示，且图中任意两个相邻的小正方体至少有一条棱（1cm）共享，或有一面（1cm×1cm）共享．老师拿出一张3cm×4cm的方格纸（如图②），请小亮将此10个小正方体依主视图摆放在方格纸中的方格内，小亮摆放后的几何体表面积最大为 cm2 ． （小正方体摆放时不得悬空，每一小正方体的棱均与水平线垂直或平行）
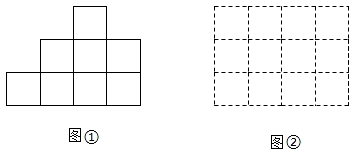16. 若干个相同的小正方体组成的几何体的主视图和左视图如图所示则组成这个几何体的小正方体最多为个．
三、解答题（共8题，共72分）
-
17. 如图所示，点P表示广场上的一盏照明灯．
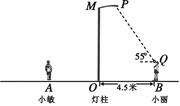(1)、请你在图中画出小敏在照明灯照射下的影子(用线段表示)；(2)、若小丽到灯柱MO的距离为4.5米，照明灯P到灯柱的距离为1.5米，小丽目测照明灯P的仰角为55°，她的目高QB为1.6米，试求照明灯P到地面的距离(结果精确到0.1米)．(参考数据：tan55°≈1.428，sin55°≈0.819，cos55°≈0.574)
18. 如图是由若干个完全相同的小正方体堆成的几何体．
(1)、图中有几个小正方体；(2)、画出该几何体的三视图；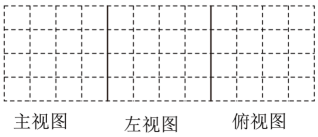
19. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如表：碟子的个数
碟子的高度（单位：cm）
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
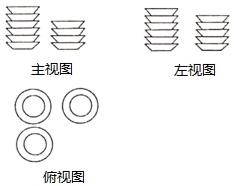(1)、当桌子上放有x个碟子时，请写出此时碟子的高度（用含x的式子表示）；(2)、分别从三个方向上看若干碟子，得到的三视图如图所示，厨房师傅想把它们整齐地叠成一摞，求叠成一摞后的高度．20. 测量金字塔高度：如图1，金字塔是正四棱锥 ，点O是正方形 的中心 垂直于地面，是正四棱锥 的高，泰勒斯借助太阳光.测量金字塔影子 的相关数据，利用平行投影测算出了金字塔的高度，受此启发，人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 表示.
(1)、测量甲金字塔高度：如图2，是甲金字塔的俯视图，测得底座正方形 的边长为 ，金字塔甲的影子是 ，此刻，1米的标杆影长为0.7米，则甲金字塔的高度为m.(2)、测量乙金字塔高度：如图1，乙金字塔底座正方形 边长为 ，金字塔乙的影子是 ， ，此刻1米的标杆影长为0.8米，请利用已测出的数据，计算乙金字塔的高度.21. 如图1，平直的公路旁有一灯杆 ， 在灯光下，小丽从灯杆的底部处沿直线前进到达点，在处测得自己的影长小丽身高 ．
(1)、求灯杆的长；(2)、若小丽从处继续沿直线前进到达处（如图2），求此时小丽的影长的长．22. 如图，一路灯AB与墙OP相距20米，当身高CD=1.6米的小亮在离墙17米的D处时，影长DG为1米；当小亮站在点F时，发现自己头顶的影子正好接触到墙的底部O处.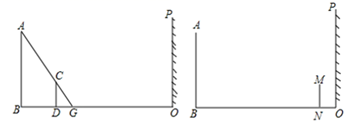
(1)、求路灯AB的高度.(2)、请在图中画出小亮EF的位置；并求出此时的影长.(3)、如果小亮继续往前走，在距离墙2米的N处停下，那么小亮MN在墙上的影子有多高？
