2022~2023学年中考数学一轮复习专题06图形的相似(基础)
试卷更新日期:2022-11-24 类型:一轮复习
一、比例线段
-
1. 已知 , 则=( )A、 B、 C、 D、2. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、143. 若长度为 , , , 的四条线段是成比例线段,则的值为( )A、2 B、4 C、16 D、34. 如图,直线 , 如果 , 那么DE的长是( )
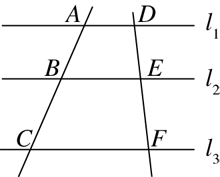 A、 B、 C、 D、5. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、 B、 C、 D、5. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E , 交AD于点F , 交CD的延长线于点G , 若AF=2FD , 则 的值为( )
A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E , 交AD于点F , 交CD的延长线于点G , 若AF=2FD , 则 的值为( ) A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则( )
A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则( )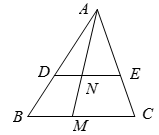 A、 B、 C、 D、8. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、 B、 C、 D、8. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )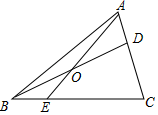 A、1:2 B、1:3 C、1:4 D、2:39. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )
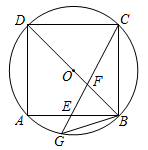
A、1:2 B、1:3 C、1:4 D、2:39. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )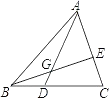 A、3:2 B、4:3 C、6:5 D、8:510. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( )
A、3:2 B、4:3 C、6:5 D、8:510. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则 的值是( )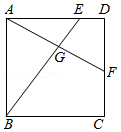 A、 B、
A、 B、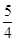 C、
C、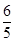 D、
D、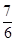
二、位似图形
-
11. 观察下列图形,这四组形状各异的图形中,是相似图形的有( )
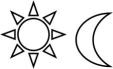



 A、1组 B、2组 C、3组 D、4组12. 下列说法正确的是( )A、位似图形可以通过平移得到 B、相似图形一定是位似图形,位似图形一定是相似图形 C、位似图形的位似中心不只有一个 D、位似中心到对应点的距离之比都相等13. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变14. 如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1∶ , 点A的坐标为(1,0),则E点的坐标为( ) .
A、1组 B、2组 C、3组 D、4组12. 下列说法正确的是( )A、位似图形可以通过平移得到 B、相似图形一定是位似图形,位似图形一定是相似图形 C、位似图形的位似中心不只有一个 D、位似中心到对应点的距离之比都相等13. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变14. 如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1∶ , 点A的坐标为(1,0),则E点的坐标为( ) .
A、( , 0) B、( , ) C、( , ) D、(2,2)15. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )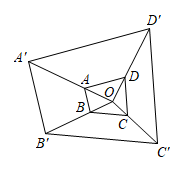 A、4 B、6 C、16 D、1816. 如图,△ABC 与△DEF 位似,点 O 是它们的位似中心,且相似比为 1:2,则△ABC 与△DEF 的周长之比是( )
A、4 B、6 C、16 D、1816. 如图,△ABC 与△DEF 位似,点 O 是它们的位似中心,且相似比为 1:2,则△ABC 与△DEF 的周长之比是( ) A、1:2 B、1:4 C、1:3 D、1:917. 如图,△ABC与△DEF位似点О为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )
A、1:2 B、1:4 C、1:3 D、1:917. 如图,△ABC与△DEF位似点О为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )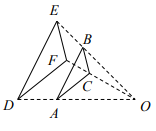 A、4 B、6 C、9 D、16
A、4 B、6 C、9 D、16三、相似的性质
-
18. 若 , , ,则 ( )A、 B、 C、 D、19. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形 DEF ,其最长边为12,则 △DEF的周长是( )A、54 B、36 C、27 D、2120. 已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )A、3:5 B、9:25 C、5:3 D、25:921. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
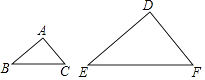 A、 = B、 = C、 = D、 =22. 如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是( )A、2:3 B、: C、4:9 D、8:2723. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么等于( ).
A、 = B、 = C、 = D、 =22. 如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是( )A、2:3 B、: C、4:9 D、8:2723. 如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么等于( ).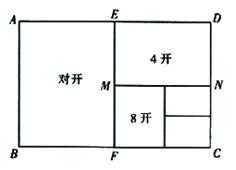 A、0.618 B、 C、 D、224. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )
A、0.618 B、 C、 D、224. 如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,与相交于点E,连接 , 则与的周长比为( )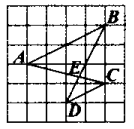 A、1:4 B、4:1 C、1:2 D、2:1
A、1:4 B、4:1 C、1:2 D、2:1四、相似的判定
-
25. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
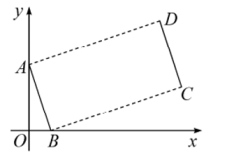 A、 B、 C、 D、26. 的边上有、、三点,各点位置如图所示.若 , , , 则根据图中标示的长度,求四边形与的面积比为何?( )
A、 B、 C、 D、26. 的边上有、、三点,各点位置如图所示.若 , , , 则根据图中标示的长度,求四边形与的面积比为何?( )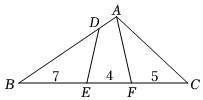 A、1:3 B、1:4 C、2:5 D、3:827. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A、1:3 B、1:4 C、2:5 D、3:827. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )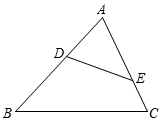 A、∠AED=∠B B、 C、AD·BC= DE·AC D、DE//BC28. 如图,等边中,点E是的中点,点D在上,且 , 则( )
A、∠AED=∠B B、 C、AD·BC= DE·AC D、DE//BC28. 如图,等边中,点E是的中点,点D在上,且 , 则( )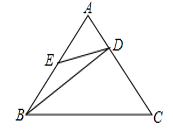 A、 B、 C、 D、29. 如图,已知点D是的边上的一点,根据下列条件,可以得到的是( )
A、 B、 C、 D、29. 如图,已知点D是的边上的一点,根据下列条件,可以得到的是( )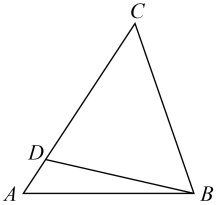 A、 B、 C、 D、30. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
A、 B、 C、 D、30. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )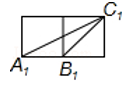 A、
A、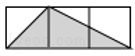 B、
B、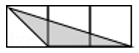 C、
C、 D、
D、 31. 已知图中有两组三角形,其边长和角的度数已在图上标注,对于各组中的两个三角形而言,下列说法正确的是( )
31. 已知图中有两组三角形,其边长和角的度数已在图上标注,对于各组中的两个三角形而言,下列说法正确的是( )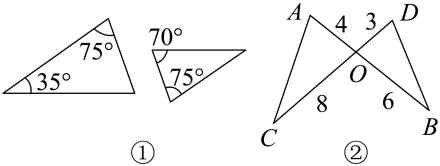 A、都相似 B、都不相似 C、只有①相似 D、只有②相似32. 已知在中, , , , 下列阴影部分的三角形与原不相似的是( )A、
A、都相似 B、都不相似 C、只有①相似 D、只有②相似32. 已知在中, , , , 下列阴影部分的三角形与原不相似的是( )A、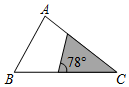 B、
B、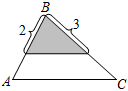 C、
C、 D、
D、 33. 如图,如果 , 那么添加下列一个条件后,仍不能确定∽的是( )
33. 如图,如果 , 那么添加下列一个条件后,仍不能确定∽的是( )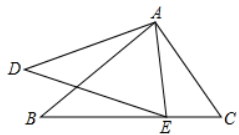 A、 B、 C、 D、34. 如图, , , , D为上一点,且 , 在上取一点E,使以A、D、E为顶点的三角形与相似,则等于( )
A、 B、 C、 D、34. 如图, , , , D为上一点,且 , 在上取一点E,使以A、D、E为顶点的三角形与相似,则等于( )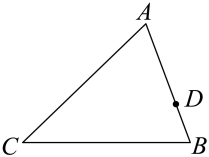 A、或 B、10或 C、或10 D、以上答案都不对35. 如图,已知∠1=∠2,添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A、或 B、10或 C、或10 D、以上答案都不对35. 如图,已知∠1=∠2,添加一个条件后,仍不能判定△ABC与△ADE相似的是( )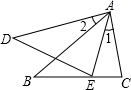 A、∠C=∠AED B、∠B=∠D C、 D、
A、∠C=∠AED B、∠B=∠D C、 D、五、黄金分割
-
36. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 下列估算正确的是( )
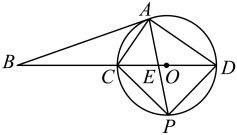
 A、 B、 C、 D、37. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、 B、 C、 D、37. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )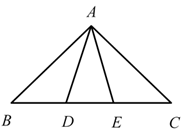 A、 B、 C、 D、38. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
A、 B、 C、 D、38. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
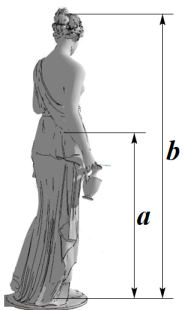 A、1.24米 B、1.38米 C、1.42米 D、1.62米39. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为 ,则小凡的身高约为( )
A、1.24米 B、1.38米 C、1.42米 D、1.62米39. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为 ,则小凡的身高约为( ) A、 B、 C、 D、40. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )
A、 B、 C、 D、40. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )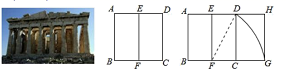 A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH41. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、42. 已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH41. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、42. 已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( ) A、AB2=AC2+BC2 B、BC2=AC•BA C、 D、
A、AB2=AC2+BC2 B、BC2=AC•BA C、 D、六、相似的应用
-
43. 如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE²=AQ·AB求证:
 (1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ44.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
(1)、∠CAE=∠BAF;(2)、CF·FQ=AF·BQ44.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.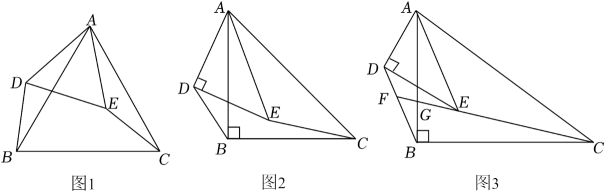 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.