2022~2023学年中考数学一轮复习专题05命题与证明

试卷更新日期：2022-11-24 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列说法错误的是（）

A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中，同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形

查看试题解析
2. 下列命题错误的是（）

A、经过直线外一点，有且只有一条直线与这条直线平行 B、负数的立方根是负数 C、对角线互相垂直的四边形是菱形 D、五边形的外角和是 $360 °$

查看试题解析
3. 下列命题为真命题的是（）

A、 $\sqrt{a^{2}} = a$ B、同位角相等 C、三角形的内心到三边的距离相等 D、正多边形都是中心对称图形

查看试题解析
4. 下列说法正确的是（）

A、一元一次方程 $\frac{x}{2} - 1 = x$ 的解是x=2 B、在连续5次数学测试中，两名同学的平均成绩相同，则方差较大的同学的成绩更稳定 C、从5名男生，2名女生中抽取3人参加活动，至少会有1名男生被抽中 D、将一次函数y=-2x+5的图象向上平移两个单位，则平移后的函数解析式为y=-2x+1

查看试题解析
5. 下列命题中，是真命题的有（）
①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形

A、①② B、①④ C、②③ D、③④

查看试题解析
6. 下列命题中，假命题是（）

A、 $- 2$ 的绝对值是-2 B、对顶角相等 C、平行四边形是中心对称图形 D、如果直线 $a ∥ c ， b ∥ c$ ，那么直线 $a ∥ b$

查看试题解析
7. 下列命题是真命题的是（）

A、对顶角相等 B、平行四边形的对角线互相垂直 C、三角形的内心是它的三条边的垂直平分线的交点 D、三角分别相等的两个三角形是全等三角形

查看试题解析
8. 如图，点 D在 △ABC的边BC上，点 P在射线 AD上（不与点 A，D重合），连接PB， PC．下列命题中，假命题是（）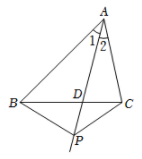

A、若 $A B = A C$ ， $A D ⊥ B C$ ，则 $P B = P C$ B、若 $P B = P C$ ， $A D ⊥ B C$ ，则 $A B = A C$ C、若 $A B = A C$ ， $∠ 1 = ∠ 2$ ，则 $P B = P C$ D、若 $P B = P C$ ， $∠ 1 = ∠ 2$ ，则 $A B = A C$

查看试题解析
9. 下列命题为真命题的是（）。

A、两条直线被一组平行线所截，所得的对应线段成比例 B、相似三角形面积之比等于相似比 C、对角线互相垂直的四边形是菱形 D、顺次连结矩形各边的中点所得的四边形是正方形

查看试题解析
10. 下列命题是假命题的是（）

A、任意一个三角形中，三角形两边的差小于第三边 B、三角形的中位线平行于三角形的第三边，并且等于第三边的一半 C、如果一个角的两边分别平行于另一个角的两边，那么这两个角一定相等 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
11. 下列命题是真命题的是（）

A、相等的两个角是对顶角 B、相等的圆周角所对的弧相等 C、若 $a < b$ ，则 $a c^{2} < b c^{2}$ D、在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是 $\frac{1}{3}$

查看试题解析
12. 下列四个选项中不是命题的是（）

A、对顶角相等 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、如果 $a = b ， a = c$ ，那么 $b = c$

查看试题解析
13. 下列命题为假命题的是（）

A、对角线相等的平行四边形是矩形 B、对角线互相垂直的平行四边形是菱形 C、有一个内角是直角的平行四边形是正方形 D、有一组邻边相等的矩形是正方形

查看试题解析
14. 下列说法正确的是（）

A、了解一批灯泡的使用寿命，应采用抽样调查的方式 B、如果某彩票的中奖概率是1%，那么一次购买100张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同， $S_{甲}^{2} = 2.5$ ， $S_{乙}^{2} = 8.7$ ，则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子，掷出的点数是7”是必然事件

查看试题解析
15. 如图，△ABC是等腰三角形，点D是底边BC上异于BC中点的一个点，∠ADE=∠DAC，DE=AC．运用这个图（不添加辅助线）可以说明下列哪一个命题是假命题？（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、有一组对边平行的四边形是梯形 C、一组对边相等，一组对角相等的四边形是平行四边形 D、对角线相等的平行四边形是矩形

查看试题解析
16. 下列判断正确的是（）

A、北斗系统第五十五颗导航卫星发射前的零件检查，应选择抽样调查 B、一组数据6，5，8，7，9的中位数是8 C、甲、乙两组学生身高的方差分别为S_甲²＝2.3，S_乙²＝1.8.则甲组学生的身高较整齐 D、命题“既是矩形又是菱形的四边形是正方形”是真命题

查看试题解析
17. 下列说法正确的是（）

A、“清明时节雨纷纷”是必然事件 B、为了了解一批灯管的使用寿命，可以采用普查的方式进行 C、一组数据2，5，4，5，6，7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 $S_{甲}^{2} = 0.02$ ， $S_{乙}^{2} = 0.01$ ，那么乙组队员的身高比较整齐

查看试题解析
18. 下列命题中是假命题的是（）

A、三角形的中位线平行于三角形的第三边，并且等于第三边的一半 B、如果两个角互为邻补角，那么这两个角一定相等 C、从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角 D、直角三角形斜边上的中线等于斜边的一半

查看试题解析
19. 下列命题：① ${(m \cdot n^{2})}^{3} = m^{3} n^{5}$ ；②数据1，3，3，5的方差为2；③因式分解 $x^{3} - 4 x = x (x + 2) (x - 2)$ ；④平分弦的直径垂直于弦；⑤若使代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x \geq 1$ ．其中假命题的个数是（）

A、1 B、3 C、2 D、4

查看试题解析
20. 以下命题：①面包店某种面包售价 $a$ 元/个，因原材料涨价，面包价格上涨10%，会员优惠从打八五折调整为打九折，则会员购买一个面包比涨价前多花了 $0.14 a$ 元；②等边三角形 $A B C$ 中， $D$ 是 $B C$ 边上一点， $E$ 是 $A C$ 边上一点，若 $A D = A E$ ，则 $∠ B A D = 3 ∠ E D C$ ；③两边及第三边上的中线对应相等的两个三角形全等；④一列自然数0，1，2，3，55，依次将该列数中的每一个数平方后除以100，得到一列新数，则原数与对应新数的差，随着原数的增大而增大．其中真命题的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
21. 已知二次函数y=x²+ax+b(a，b为常数)．命题①：该函数的图象经过点(1，0)；命题②：该函数的图象经过点(3，0)；命题③：该函数的图象与x轴的交点位于y轴的两侧；命题④；该函数的图象的对称轴为直线x=1．如果这四个命题中只有一个命题是假命题，则这个假命题是（）

A、命题① B、命题② C、命题③ D、命题④

查看试题解析
22. 下列命题中，假命题是（）

A、直角三角形斜边上的中线等于斜边的一半 B、等腰三角形顶角的平分线，底边上的中线，底边上的高相互重合 C、若 $A B = B C$ ，则点B是线段AC的中点 D、三角形三条边的垂直平分线的交点叫做这个三角形的外心

查看试题解析
23. 下列命题中，为真命题的是（）
（1）对角线互相平分的四边形是平行四边形（2）对角线互相垂直的四边形是菱形（3）对角线相等的平行四边形是菱形（4）有一个角是直角的平行四边形是矩形

A、（1）（2） B、（1）（4） C、（2）（4） D、（3）（4）

查看试题解析
24. 定理：三角形的一个外角等于与它不相邻的两个内角的和．
已知：如图， $∠ A C D$ 是 $△ A B C$ 的外角．

求证： $∠ A C D = ∠ A + ∠ B$ ．

下列说法正确的是（）

A、证法1还需证明其他形状的三角形，该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证，就能证明该定理

查看试题解析
25. 能说明“锐角 $α$ ，锐角 $β$ 的和是锐角”是假命题的例证图是（）.

A、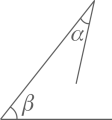 B、 C、 D、

查看试题解析
26. 判断命题“如果n＜1，那么n²﹣1＜0”是假命题，只需举出一个反例.反例中的n可以为（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、0 D、 $\frac{1}{2}$

查看试题解析
27. 用反证法证明时，假设结论“点在圆外”不成立，那么点与圆的位置关系只能是（）

A、点在圆内 B、点在圆上 C、点在圆心上 D、点在圆上或圆内

查看试题解析
28. 如图，已知 $P A ， P B$ 是 $⊙ O$ 的两条切线，A ， B为切点，线段 $O P$ 交 $⊙ O$ 于点M ．给出下列四种说法：① $P A = P B$ ；② $O P ⊥ A B$ ；③四边形 $O A P B$ 有外接圆；④M是 $△ A O P$ 外接圆的圆心，其中正确说法的个数是（）

A、1 B、2 C、3 D、4

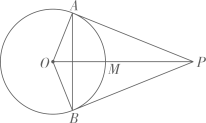查看试题解析
29. 命题①设 $△ A B C$ 的三个内角为A、B、C且 $α = A + B ， β = C + A ， γ = C + B$ ，则 $α$ 、 $β$ 、 $γ$ 中，最多有一个锐角；②顺次连接菱形各边中点所得的四边形是矩形；③从11个评委分别给出某选手的不同原始评分中，去掉1个最高分、1个最低分，剩下的9个评分与11个原始评分相比，中位数和方差都不发生变化．其中错误命题的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
30. 用三个不等式 $a > b$ ， $a b > 0$ ， $\frac{1}{a} < \frac{1}{b}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
31. 给出下列5个命题：①两点之间直线最短；②同位角相等；③等角的补角相等；④不等式组 ${\begin{matrix} x > - 2 \\ x < 2 \end{matrix}$ 的解集是﹣2＜x＜2；⑤对于函数y=﹣0.2x+11，y随x的增大而增大．其中真命题的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
32. 下列命题中：
①如果a＞b，那么a²＞b²②一组对边平行，另一组对边相等的四边形是平行四边形③从圆外一点可以引圆的两条切线，它们的切线长相等④关于x的一元二次方程ax²+2x+1=0有实数根，则a的取值范围是a≤1其中真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
33. 下列说法错误的是（）

A、通过平移或旋转得到的图形与原图形全等 B、“对顶角相等”的逆命题是真命题 C、圆内接正六边形的边长等于半径 D、“经过有交通信号灯的路口，遇到红灯”是随机事件

查看试题解析
34. 已知下列命题：
①若a³＞b³ ，则a²＞b²；②若点A（x₁ ， y₁）和点B（x₂ ， y₂）在二次函数y=x²﹣2x﹣1的图象上，且满足x₁＜x₂＜1，则y₁＞y₂＞﹣2；③在同一平面内，a，b，c是直线，且a∥b，b⊥c，则a∥c；④周长相等的所有等腰直角三角形全等．其中真命题的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
35. 下列命题中，假命题有（）
①两点之间线段最短；②到角的两边距离相等的点在角的平分线上；
③过一点有且只有一条直线与已知直线平行；④垂直于同一直线的两条直线平行；
⑤若⊙O的弦AB，CD交于点P，则PA•PB=PC•PD．

A、4个 B、3个 C、2个 D、1个

查看试题解析
36. 已知下列命题：
①若 $\frac{a}{b}$ ＞1，则a＞b；
②若a+b=0，则|a|=|b|；
③等边三角形的三个内角都相等；
④底角相等的两个等腰三角形全等．
其中原命题与逆命题均为真命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
37. 给出下列命题：①若m=n+1，则1﹣m²+2mn﹣n²=0；②对于函数y=kx+b（k≠0），若y随x的增大而增大，则其图象不能同时经过第二、四象限；③若a、b（a≠b）为2、3、4、5这四个数中的任意两个，则满足2a﹣b＞4的有序数组（a，b）共有5组．其中所有正确命题的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
38. 已知⊙O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：
①若d＞5，则m=0；②若d=5，则m=1；③若1＜d＜5，则m=3；④若d=1，则m=2；⑤若d＜1，则m=4．
其中正确命题的个数是（）

A、1 B、2 C、3 D、5

查看试题解析

二、填空题

39. 下列四个命题中：①对顶角相等；②同旁内角互补；③全等三角形的对应角相等；④两直线平行，同位角相等，其中假命题的有（填序号）

查看试题解析
40. 判断命题“代数式 $2 m^{2} - 1$ 的值一定大于代数式 $m^{2} - 1$ 的值”是假命题，只需举出一个反例，反例中m的值为．

查看试题解析
41. 命题“如果|a|=|b|，那么a=b．”的逆命题是．

查看试题解析
42. 下列四个命题中，正确的是（填写正确命题的序号）
①三角形的外心是三角形三边垂直平分线的交点；
②函数y=（1﹣a）x²﹣4x+6与x轴只有一个交点，则a= $\frac{1}{3}$ ；
③半径分别为1和2的两圆相切，则两圆的圆心距为3；
④若对于任意x＞1的实数，都有ax＞1成立，则a的取值范围是a≥1．

查看试题解析
43. 下列说法错误的是（只填序号）
① $7 - \sqrt{17}$ 的整数部分为2，小数部分为 $\sqrt{17} - 4$ ．

②外角为 $60 °$ 且边长为2的正多边形的内切圆的半径为 $\sqrt{3}$ ．

③把直线 $y = 2 x - 3$ 向左平移1个单位后得到的直线解析式为 $y = 2 x - 2$ ．

④新定义运算： $m * n = m n^{2} - 2 n - 1$ ，则方程 $- 1 * x = 0$ 有两个不相等的实数根．

查看试题解析
44. 如图，图中二次函数解析式为y=ax²+bx+c（a≠0）则下列命题中正确的有（填序号）
①abc＞0；②b²＜4ac；③4a﹣2b+c＞0；④2a+b＞c．

查看试题解析