2022~2023学年中考数学一轮复习专题03因式分解

试卷更新日期：2022-11-24 类型：一轮复习

进入出卷网下载

一、单选题

1. 下面各式从左到右的变形，属于因式分解的是（）

A、 $x^{2} - x - 1 = x (x - 1) - 1$ B、 $x^{2} - 1 = (x - 1)^{2}$ C、 $x^{2} - x - 6 = (x - 3) (x + 2)$ D、 $x (x - 1) = x^{2} - x$

查看试题解析
2. 下列由左边到右边的变形是因式分解的是（）

A、 $(a + 3) (a - 3) = a^{2} - 9$ B、 $a^{2} - b^{2} + 1 = (a + b) (a - b) + 1$ C、 $a^{2} + b^{2} = {(a + b)}^{2}$ D、 $4 a^{2} - 9 = (2 a + 3) (2 a - 3)$

查看试题解析
3. 下列多项式中，能用平方差公式进行因式分解的是（）

A、a²﹣b² B、﹣a²﹣b² C、a²+b² D、a²+2ab+b²

查看试题解析
4. 下列分解因式正确的是（）

A、 $x^{2} - 3 x + 1 = x (x - 3) + 1$ B、 $x^{2} - 2 x + 1 = x (x - 2 + \frac{1}{x})$ C、 $(m + n)^{2} = m^{2} + 2 m n + n^{2}$ D、 $- a^{3} + a = - a (a + 1) (a - l)$

查看试题解析
5. 多项式 $39 x^{2} + 5 x - 14$ 可因式分解成 $(3 x + a) (b x + c)$ ，其中 $a$ 、 $b$ 、 $c$ 均为整数，求 $a + 2 c$ 之值为何？（）

A、-12 B、-3 C、3 D、12

查看试题解析
6. 已知多项式 $2 x^{3} - x^{2} + m$ 分解因式后有一个因式是 $x + 1$ ，则 $m$ 的值为（）

A、3 B、-3 C、1 D、-1

查看试题解析
7. 我们知道 $6 - \sqrt{2}$ 的小数部分b为 $2 - \sqrt{2}$ ，如果用a代表它的整数部分，那么 $a b^{2} - a^{2} b$ 的值是（）

A、8 B、－8 C、4 D、－4

查看试题解析

二、填空题

8. 已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m²﹣n²的值是．

查看试题解析
9. 因式分解： $3 x^{3} - 12 x y^{2} =$ ．

查看试题解析
10. 分解因式：a⁴﹣3a²﹣4＝.

查看试题解析
11. 分解因式： $2 x^{3} + 4 x^{2} + 2 x =$ ．

查看试题解析
12. 因式分解： ${(m + n)}^{2} - 6 (m + n) + 9 =$ ．

查看试题解析
13. 因式分解： $x^{2} - x^{4} =$ .

查看试题解析
14. 已知 $m^{2} + n^{2} + 10 = 6 m - 2 n$ ，则 $m - n =$ .

查看试题解析

三、综合题

15. 某校数学社团的小亮、小颖两个同学利用分组分解法进行的因式分解：
小亮： $m^{2} - m n + 2 m - 2 n$
= $(m^{2} - m n) + (2 m - 2 n)$
= $m (m - n) + 2 (m - n)$
= $(m - n) (m + 2)$
小颖： $4 x^{2} - y^{2} - z^{2} + 2 y z$
$= 4 x^{2} - (y^{2} + z^{2} - 2 y z)$
= $2 x^{2} - (y - z)^{2}$
$= (2 x + y - z) (2 x - y + z)$ ．
请你在他们解法的启发下，解决下面问题；

(1)、因式分解 $a^{3} - 3 a^{2} - 9 a + 27$ ；

(2)、因式分解 $x^{2} - 4 x y + 4 y^{2} - 16$ ；

(3)、已知a，b，c是 $Δ A B C$ 的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $Δ A B C$ 的形状并说明理由．

查看试题解析
16. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
17. 如图，将一张矩形纸板按照图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m>n，(以上长度单位：cm)

(1)、观察图形，可以发现代数式2m²＋5mn＋2n²可以因式分解为；

(2)、若每块小矩形的面积为10 cm² ，四个正方形的面积和为58 cm² ，试求图中所有裁剪线(虚线部分)长之和．

查看试题解析
18. 八年级课外兴趣小组活动时，老师提出了如下问题：
将 $2 a - 3 a b - 4 + 6 b$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $= (2 a - 3 a b) - (4 - 6 b) = a (2 - 3 b) - 2 (2 - 3 b) = (2 - 3 b) (a - 2)$
解法二：原式 $= (2 a - 4) - (3 a b - 6 b) = 2 (a - 2) - 3 b (a - 2) = (a - 2) (2 - 3 b)$
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

(1)、【类比】
请用分组分解法将 $x^{2} - a^{2} + x + a$ 因式分解；

(2)、【挑战】
请用分组分解法将 $a x + a^{2} - 2 a b - b x + b^{2}$ 因式分解；

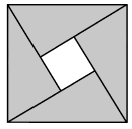
(3)、【应用】
“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a和 $b (a > b)$ ，斜边长是3，小正方形的面积是1．根据以上信息，先将 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值．

查看试题解析
19. ［阅读材料]
下面是某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行因式分解的过程．
设 $x^{2} - 4 x = y$
原式= $(y + 2) (y + 6) + 4$ （第一步）
$= y^{2} + 8 y + 16$ （第二步）
$= {(y + 4)}^{2}$ （第三步）
$= (x^{2} - 4 x + 4)^{2}$ （第四步）
请问：

(1)、该同学因式分解的结果是否符合题意？若不符合题意，请直接写出因式分解的最后结果．

(2)、请你模仿以上方法尝试对多项式 $(a^{2} - 2 a) (a^{2} - 2 a + 2) + 1$ 进行因式分解．

查看试题解析
20. 阅读下列因式分解的过程，再回答所提出的问题：
$1 + x + x (x + 1) + x (x + 1)^{2}$
$= (1 + x) [1 + x + x (x + 1)]$
$= (1 + x)^{2} (1 + x)$
$= (1 + x)^{3}$

(1)、上述分解因式的方法是．

(2)、若分解 $1 + x + x (x + 1) + x (x + 1)^{2} + ⋯ + x (x + 1)^{2021}$ ，则结果是．

(3)、依照上述方法分解因式： $1 + x + x (x + 1) + x (x + 1)^{2} + ⋯ + x (x + 1)^{n}$ （n为正整数）．

查看试题解析
21. 先阅读下面的内容，再解决问题．
如果一个整式 $A$ 等于整式 $B$ 与整式 $C$ 之积，则称整式 $B$ 和整式 $C$ 为整式 $A$ 的因式．
如：①因为 $36 = 4 \times 9$ ，所以4和9是36的因数；
因为 $x^{2} - x - 2 = (x + 1) (x - 2)$ ，所以 $x + 1$ 和 $x - 2$ 是 $x^{2} - x - 2$ 的因式．
②若 $x + 1$ 是 $x^{2} + a x - 2$ 的因式，则求常数 $a$ 的值的过程如下：
解：∵ $x + 1$ 是 $x^{2} + a x - 2$ 的因式，
∴存在一个整式 $(m x + n)$ ，使得 $x^{2} + a x - 2 = (x + 1) (m x + n)$ ，
∵当 $x = - 1$ 时， $(x + 1) (m x + n) = 0$ ，
∴当 $x = - 1$ 时， $x^{2} + a x - 2 = 0$ ，
∴ $1 - a - 2 = 0$ ，
∴ $a = - 1$ ．

(1)、若 $x + 5$ 是整式 $x^{2} + m x - 10$ 的一个因式，则 $m =$ ．

(2)、若整式 $x^{2} - 1$ 是 $3 x^{4} - a x^{2} + b x + 1$ 的因式，求 $\sqrt{a + 2017 b}$ 的值．

查看试题解析
22. 先阅读下列材料：我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．
拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．如：
x²＋2x﹣3＝x²＋2x＋1﹣4＝（x＋1）²﹣2²＝（x＋1＋2）（x＋1﹣2）＝（x＋3）（x﹣1）
请你仿照以上方法，探索并解决下列问题：

(1)、分解因式：x²﹣6x﹣7；

(2)、分解因式：a²＋4ab﹣5b²

查看试题解析
23. 如图1，有若干张边长为α的小正方形①，长为b、宽为α的长方形②以及边长为b的大正方形3的纸片.

(1)、已知小正方形1与大正方形3的面积之和为169，长方形②的周长为34，求长方形2的面积；

(2)、如果现有小正方形①2张，大正方形31张，长方形②3张，请你将它们拼成一个大长方形(在图2虚线框内画出图形)，并运用面积之间的关系，将多项式 $2 a^{2} + 3 a b + b^{2}$ 分解因式.

查看试题解析
24. 如图，将一张大长方形纸板按图中虚线裁剪成9块，其中有2块是边长为a厘米的大正方形，2块是边长都为b厘米的小正方形，5块是长为a厘米，宽为b厘米的相同的小长方形，且 $a > b$ ．

(1)、观察图形，可以发现代数式 $2 a^{2} + 5 a b + 2 b^{2}$ 可以因式分解为．

(2)、若图中阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米，求图中空白部分的面积．

查看试题解析