云南省楚雄彝族自治州双柏县2022-2023学年八年级上学期期中数学试题
试卷更新日期：2022-11-24 类型：期中考试
一、单选题
-
1. 以下列各组线段长为边，能构成三角形的是（ ）A、1 cm，6 cm，5 cm B、8 cm，7 cm，7 cm C、4 cm，4 cm，9 cm D、7 cm，8 cm，17 cm2. 等腰三角形是轴对称图形，它的对称轴是（ ）A、中线 B、底边上的中线 C、底边上的高 D、底边上的中线所在的直线3. 已知一个多边形的内角和为1080°，则这个多边形是（ ）A、九边形 B、八边形 C、七边形 D、六边形4. 下列大学的校徽图案是轴对称图形的是（ ）A、
清华大学
B、
北京大学
C、
中国人民大学
D、
浙江大学
5. 如图，AD、BE分别是△ABC的角平分线和高线，若∠ABE=26°，则∠CAD的度数为（ ）
A、32° B、35° C、37° D、64°6. 如图，AC与BD相交于点O，OA=OD，OB=OC，不添加辅助线，判定△ABO≌△DCO的依据是（ ）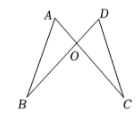
A、SSS B、SAS C、AAS D、HL7. 如图，在中， ， 于点D，若 ， 则（ ）
A、8 B、4 C、4 D、48. 如图，若△ABC≌△DEF，四个点B、E、C、F在同一直线上，BC＝7，EC＝5，则CF的长是（ ）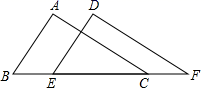
A、2 B、3 C、5 D、79. 如图，在中，的平分线交于点是中点，且 ， 那么的度数为（ ）
A、 B、 C、 D、10. 等腰三角形中，有一个角是40°，它的一条腰上的高与底边的夹角是（ ）A、 B、 C、或 D、或11. 在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°﹣∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个12. 如图，下列4个三角形中，均有AB=AC，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（ ）
A、①③ B、①②④ C、①③④ D、①②③④二、填空题
-
13. 点P(2，-5)关于x轴对称的点的坐标为14. 三角形的三边长分别为3、8、x，则x的取值范围是.15. 如图所示，在四边形中，则的长为cm．
16. 在中， ， 的外角等于 ， 则的度数是 ．17. 若正多边形的一个外角是45°，则该正多边形的边数是 ．18. 已知等腰三角形两边长分别为3cm和5cm，则等腰三角形的周长为cm．三、解答题
-
19.
如图，C是线段AB的中点，CD=BE，CD∥BE．求证：∠D=∠E．
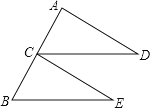20. 如图，在△ABC中，AD平分∠BAC，AE⊥BC，若∠BAD＝40°，∠C＝70°，求∠DAE的度数．
21. 一个多边形的内角和比外角和的3倍少180°.求：(1)、这个多边形的边数；(2)、该多边形共有多少条对角线.22. 如图，已知：AB⊥BD，ED⊥BD，AB＝CD，AC＝CE.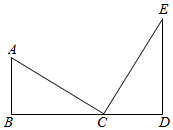
(1)、AC与CE有什么位置关系？(2)、请证明你的结论.23.如图，△ABC中，AD⊥BC于点D，BE平分∠ABC，若∠ABC=64°，∠AEB=70°．
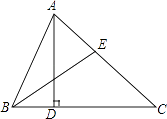(1)、求∠CAD的度数；(2)、若点F为线段BC上的任意一点，当△EFC为直角三角形时，求∠BEF的度数．24. 如图所示，在中， ， 现有两点M，N分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为 ， 点N的速度为 ． 当点N第一次到达点B时，M，N同时停止运动．
(1)、运动几秒后，M，N两点重合？(2)、点M，N运动几秒后，可得到等边三角形？(3)、当点M，N在边上运动时，是否存在以为底边的等腰三角形？若存在，请求出此时M，N运动的时间．