山西省吕梁孝义市2022-2023学年八年级上学期期中质量监测年级数学试题
试卷更新日期:2022-11-24 类型:期中考试
一、单选题
-
1. 下列各组图案中,不是全等形的是( )A、
 B、
B、 C、
C、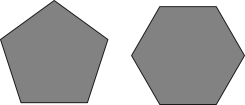 D、
D、 2. 下图是天气预报中的图形,其中是轴对称图形的是( )A、
2. 下图是天气预报中的图形,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 十边形的内角和为( )A、180° B、360° C、1800° D、1440°4. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 如图,已知点A,D,C,F在同一直线上, , , 添加下列条件后,仍不能判断的是( )
3. 十边形的内角和为( )A、180° B、360° C、1800° D、1440°4. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 如图,已知点A,D,C,F在同一直线上, , , 添加下列条件后,仍不能判断的是( ) A、 B、 C、 D、6. 数学活动课上,小明一笔画成了如图所示的图形,则的度数为( )
A、 B、 C、 D、6. 数学活动课上,小明一笔画成了如图所示的图形,则的度数为( ) A、360° B、540° C、720° D、无法计算7. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌).下列正多边形中,可以单独镶嵌平面的是( )A、正五边形 B、正六边形 C、正七边形 D、正八边形8.
A、360° B、540° C、720° D、无法计算7. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌).下列正多边形中,可以单独镶嵌平面的是( )A、正五边形 B、正六边形 C、正七边形 D、正八边形8.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
 A、PA=PB B、PO平分∠APB C、OA=OB D、AB垂直平分OP9. 等腰 中, ,用尺规作图作出线段BD,则下列结论错误的是( )
A、PA=PB B、PO平分∠APB C、OA=OB D、AB垂直平分OP9. 等腰 中, ,用尺规作图作出线段BD,则下列结论错误的是( ) A、 B、 C、 D、 的周长10. 如图,点P在的内部,点M,N分别是点P关于直线 , 的对称点,线段交 , 于点E,F,若 , 则的度数是( )
A、 B、 C、 D、 的周长10. 如图,点P在的内部,点M,N分别是点P关于直线 , 的对称点,线段交 , 于点E,F,若 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 港珠澳大桥全长约55公里,集桥、岛、隧于一体,是连接香港、珠海和澳门的超大型跨海通道,是迄今世界最长的跨海大桥.如图是港珠澳大桥中的斜拉索桥,索塔、斜拉索、桥面构成了三角形,这样使其更稳定,其中运用的数学原理是 .
 12. 若一个多边形的内角和为1800°,则这个多边形的对角线条数是 .13. 如图是一个平分角的仪器,其中 , , 将点A放在角的顶点,和沿着角的两边放下,沿画一条射线 , 就是的平分线,这样做的依据是 .
12. 若一个多边形的内角和为1800°,则这个多边形的对角线条数是 .13. 如图是一个平分角的仪器,其中 , , 将点A放在角的顶点,和沿着角的两边放下,沿画一条射线 , 就是的平分线,这样做的依据是 . 14. 如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间, , , 若每个小长方体教具高度均为4cm,则两摞长方体教具之间的距离的长为cm.
14. 如图,小张同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间, , , 若每个小长方体教具高度均为4cm,则两摞长方体教具之间的距离的长为cm. 15. 一种拉杆式旅行箱的示意图如图所示,箱体长 , 拉杆最大伸长距离 , (点在同一条直线上),在箱体的底端装有一圆形滚轮,滚轮中心到地面的距离 . 当人的手自然下垂拉旅行箱时,人感觉较为舒服.已知小亮的手自然下垂在点C处且拉杆达到最大延伸距离时,旅行箱与小亮身体的夹角为 , , 则此时小亮的手到地面的距离为 .
15. 一种拉杆式旅行箱的示意图如图所示,箱体长 , 拉杆最大伸长距离 , (点在同一条直线上),在箱体的底端装有一圆形滚轮,滚轮中心到地面的距离 . 当人的手自然下垂拉旅行箱时,人感觉较为舒服.已知小亮的手自然下垂在点C处且拉杆达到最大延伸距离时,旅行箱与小亮身体的夹角为 , , 则此时小亮的手到地面的距离为 .
三、解答题
-
16. 如图,已知中,是边上的高,平分 , 与相交于点P, , , 求和的度数.
 17. 如图,点B,C在上, , , . 求证: .
17. 如图,点B,C在上, , , . 求证: . 18. 作图题.
18. 作图题.如图,已知 , 点C是上一点.

实践与操作:
①过点C在的右侧作射线 , 使;
②作的平分线;记与的交点为M.(尺规作图,不写作法,保留作图痕迹)
猜想与探究:
猜想与有怎样的数量关系,并说明理由.
19. 如图,在ABC中,点D是AB边的中点,且CD=AB,求证:∠ACB=90°. 20. 如图,在中,已知点 , , .
20. 如图,在中,已知点 , , . (1)、作出关于y轴对称的 , (点 , , 分别是点A,B,C的对应点)并写出点 , , 的坐标:;(2)、作出向右平移6个单位后的 , (点 , , 分别是点A,B,C的对应点)并写出点 , , 的坐标,;(3)、观察和 , 它们是否关于某条直线对称?若是,请在图中直接画出对称轴,不留痕迹.21. 请认真阅读下列材料,并完成相应学习任务.
(1)、作出关于y轴对称的 , (点 , , 分别是点A,B,C的对应点)并写出点 , , 的坐标:;(2)、作出向右平移6个单位后的 , (点 , , 分别是点A,B,C的对应点)并写出点 , , 的坐标,;(3)、观察和 , 它们是否关于某条直线对称?若是,请在图中直接画出对称轴,不留痕迹.21. 请认真阅读下列材料,并完成相应学习任务.探索四边形的内角和
数学课上,老师提出如下问题:我们知道,三角形的内角和等于 , 正方形、长方形的内角和都等于 . 那么,任意一个四边形的内角和是否也等于呢?你能利用三角形内角和定理证明四边形的内角和等于吗?
“勤奋小组”的思路是:如图1,连接对角线 , 则四边形被分为两个三角形,即和 . 由此可得,∵ ,
∴ . 即四边形的内角和是360°.


“智慧小组”受到“勤奋小组”的启发,他们发现,在四边形的一条边上取一点E,或在四边形内部取一点E,也可以将四边形分为几个三角形(如图2或图3),进而证明四边形内角和等于360°.
“创新小组”的思路是:如图4,在四边形外部取一点E,分别连接 , , , …
(1)、任务一:勤奋小组在探索四边形内角和的过程中,主要体现的数学思想是( )
A、从一般到特殊 B、转化 C、抽象(2)、任务二:在图2和图3中,选择一种,按照智慧小组的思路.求证:;
(3)、任务三:如图4,请按照创新小组的思路求证: .
22. 综合与实践综合实践课上,老师让同学们提出下面数学问题并解答:
问题情境:中, , , 于点D,点M为直线上一点,过点M作 , 垂足为点E,交于点F.试探究与的数量关系.
 (1)、数学思考:
(1)、数学思考:“兴趣小组”发现,如图1,当点M与点A重合时, , 并给出如下证明过程:
∵于点D,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵在中, , ,
∴ ,
∴ ,
∴ , (依据1)
∴ ,
∵中, , ,
∴ , (依据2),
∴ , 即;
上述证明过程中,“依据1”,“依据2”分别指的是:
依据1:;
依据2: .
(2)、 类比探究“智慧小组”认为:如图2,当点M是边上一点时(与A,C不重合),“兴趣小组”发现的结论仍然成立,请你证明.
(3)、 拓展延伸请你思考:如图3,当点M是延长线一点时,“兴趣小组”发现的结论是否成立?若成立,请在图3中作出辅助线,不必证明;若不成立,说明理由.