山东省滨州市滨城区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 16平方根是（）

A、 4 B、﹣4 C、±4 D、±8

查看试题解析
2. 已知三角形三边长分别为 3，x，14，若 x 为正整数，则这样的三角形个数为（）

A、4 B、5 C、6 D、7

查看试题解析
3. 下列生活实物中，没有应用到三角形的稳定性的是（　　）

A、 B、 C、 D、

查看试题解析
4. 如图，D是 $△ A B C$ 的 $B C$ 边上一点， $∠ B = ∠ 1$ ， $∠ 3 = 80 °$ ， $∠ B A C = 70 °$ ．则 $∠ 2$ 的大小是（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $35 °$

查看试题解析
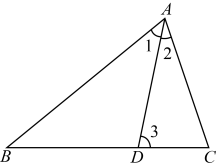5. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图，在 $∠ A O B$ 的两边 $O A$ 、 $O B$ 上分别在取 $O C = O D$ ，移动角尺，使角尺两边相同的刻度分别与点 $C$ 、 $D$ 重合，这时过角尺顶点 $M$ 的射线 $O M$ 就是 $∠ A O B$ 的平分线.这里构造全等三角形的依据是（）

A、 $S A S$ B、 $A S A$ C、 $A A S$ D、 $S S S$

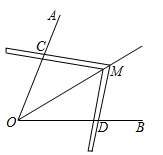查看试题解析
6. 温江进行河边公园改造，如图，江安河公园有三角形草坪（△ABC），现准备在该三角形草坪内种一棵树，使得该树到△ABC三个顶点的距离相等，则该树应种在（　　）

A、三条边的垂直平分线的交点 B、三个角的角平分线的交点 C、三角形三条高的交点 D、三角形三条中线的交点

查看试题解析
7. 如图，已知 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ，在直线 $B C$ 或射线 $A C$ 取一点P，使得 $△ P A B$ 是等腰三角形，则符合条件的点P有（）

A、2个 B、4个 C、5个 D、6个

查看试题解析
8. 若不等式组 ${\begin{array}{l} x \geq - b \\ 1 - 2 x > x - 2 \end{array}$ 无解，则实数b的取值范围是（）

A、 $b \leq - 1$ B、 $b \geq - 1$ C、 $b < - 1$ D、 $b > - 1$

查看试题解析
9. 下列选项可用 $S A S$ 证明 $△ A B C ≅ △ A^{'} B^{'} C^{'}$ 的是（）

A、 $A B = A^{'} B^{'}$ ， $∠ B = ∠ B^{'}$ ， $A C = A^{'} C^{'}$ B、 $A B = A^{'} B^{'}$ ， $B C = B^{'} C^{'}$ ， $∠ A = ∠ A^{'}$ C、 $A C = A^{'} C^{'}$ ， $B C = B^{'} C^{'}$ ， $∠ C = ∠ C^{'}$ D、 $A C = A^{'} C^{'}$ ， $B C = B^{'} C^{'}$ ， $∠ B = ∠ B^{'}$

查看试题解析
10. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90 °$ ， $∠ B = 30 °$ ， $A D ⊥ B C$ ．则下列等式成立的是（）

A、 $B D = 3 D C$ B、 $A D = 2 D C$ C、 $A B = 4 D C$ D、 $B D = 2 A C$

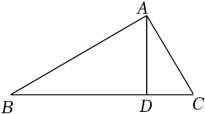查看试题解析
11. 如图，要在街道l设立一个牛奶站O，向居民区A，B提供牛奶，下列设计图形中使 $O A + O B$ 值最小的是（）

A、 B、 C、 D、

查看试题解析
12. 如图，已知 $△ A B C$ 中， $∠ A = 60 °$ ， $B E$ ， $C D$ 分别平分 $∠ A B C$ ， $∠ A C B$ ， $P$ 为 $B E$ ， $C D$ 的交点，则以下结论中(1) $∠ B P C = 120 °$ ， (2) $B D + C E = B C$ ， (3) $S_{△ P B D} + S_{△ P C E} = S_{△ P B C}$ ， (4)连接 $A P ， A P$ 平分 $∠ B A C$ ，正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

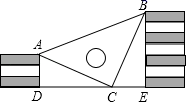
13. △ABC中，AB＝AC，∠A＝∠C，则∠B＝度．

查看试题解析
14. 在平面直角坐标系中，若点 $A (a ， b)$ 与点 $B (1 ， - 2)$ 关于y轴对称，则 $a - b =$ ．

查看试题解析
15. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是二元一次方程组 ${\begin{array}{l} 3 x + 2 y = m \\ n x - y = 1 \end{array}$ 的解，则m+n的值是．

查看试题解析
16. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC＝BC，∠ACB＝90°)，点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm.

查看试题解析
17. 如图所示，P是等边三角形 $A B C$ 内一点，将 $△ A B P$ 绕点B顺时针方向旋转 $60 °$ ，得到 $△ C B P^{^{'}}$ ，若 $P B = 3$ ，则 $P P^{'} =$ ．

查看试题解析
18. 如图， $△ A B D$ ， $△ A E C$ 都是等边三角形， $B E$ ， $C D$ 相交于点O．① $B E = D C$ ；② $∠ B O C = 60 °$ ；③ $A O$ 平分 $∠ D O E$ ；④ $A O$ 平分 $∠ B A C$ ，则以下结论中正确的是（填序号）．

查看试题解析

三、解答题

19. 解下列方程组：

(1)、 ${\begin{array}{l} x + 3 y = 8 \\ 5 x - 3 y = 4 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x}{3} + 1 = y \\ 2 (x + 1) - y = 6 \end{array}$ ；

(3)、解不等式 $2 x - 5 < 4 (x + 1) - 3$ ，并写出它的负整数解；

(4)、解不等式组 ${\begin{array}{l} 2 x - 7 > - 15 \\ \frac{7 x + 1}{5} - 1 \leq x \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
20. 如图，在平面直角坐标系中，A（ $- 2$ ， 2），B（ $- 4$ ， $- 2$ ）

(1)、用无刻度直尺作出线段AB的垂直平分线．

(2)、将点B先向右平移9个单位再向上平移1个单位得到点C，则点C的坐标为．

(3)、点D与点A关于y轴对称，在直角坐标系中找一点P，使它到A、D、C三点距离相等，则P点坐标为．

查看试题解析
21. 如图，△ABC中，BD是角平分线，∠ABC=∠C=∠BDC，求∠A的度数．

查看试题解析
22. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D E$ 、 $D F$ 分别是 $△ A B D$ 和 $△ A C D$ 的高．

(1)、请说明 $A E = A F$ 的理由；

(2)、若 $A B - A C = 2$ ， $C F = 1$ ，求线段 $B E$ 的长．

查看试题解析
23. 十一节前夕，某商店从厂家购进A、B两种礼盒，已知购买A种礼盒5个，B种礼盒2个共花费640元，购买一个B种制盒比购买一个A种盒多花40元．

(1)、求A、B两种礼盒的单价分别是多少元？

(2)、该商店购进这两种礼盒恰好用去8800元，且购进A种礼盒最多32个，B种礼盒的数量不超过A种礼盒数量的2倍，共有哪几种进货方案？

查看试题解析
24. 综合与实践：
已知在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、【特殊情况，探索结论】
如图①，当点E为 $A B$ 的中点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ （填“>”“<”或“=”）．

(2)、【特例启发，解答题目】
如图②，当点E为 $A B$ 边上任意一点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论， $A E$ $D B$ （填“>”“<”或“=”）；理由如下：过点E作 $E F ∥ B C$ ，交 $A C$ 于点F．（请你完成后面解答过程）．

(3)、【拓展结论，深入探究】
在等边三角形 $A B C$ 中，点E在直线 $A B$ 上，点D在直线 $B C$ 上，且 $E D = E C$ ．若 $△ A B C$ 的边长为1， $A E = 2$ ，求CD的长．（请你画出相应图形，并写出解答过程）

查看试题解析