江西省抚州市南城县2022-2023学年八年级上学期期中考数学试卷

试卷更新日期：2022-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中的无理数是（）

A、0.7 B、 C、π D、－8

查看试题解析
2. 在平面直角坐标系中，点 $A (- 2 ， - 3)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在Rt△ABC中，∠C＝90°，AB＝13，AC＝12，则△ABC的面积为（）

A、5 B、60 C、45 D、30

查看试题解析
4. 一次函数 $y = - \frac{1}{2} x + n$ 图像上有两点 $A (- 2 ， y_{1})$ ， $B (3 ， y_{2})$ ，则 $y_{1}$ 、 $y_{2}$ 的大小关系为（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法确定

查看试题解析
5. 实数a，b在数轴上的位置如图所示，则下列判断错误的是（）

A、 $a < b$ B、 $| a | < | b |$ C、 $- a > - b$ D、 $a + b < 0$

查看试题解析
6. 两个一次函数 $y = a x + b$ 和 $y = b x + a$ 在同一平面直角坐标系中的图象可能是（　）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 化简： $\sqrt{\frac{2}{5}}$ =

查看试题解析
8. 一次函数 $y = - 3 x + 1$ 图象不经过第象限．

查看试题解析
9. 若 $y = \sqrt{x - 3} + \sqrt{3 - x} + 2$ ，则 $x + y =$ ．

查看试题解析
10. 一轮船以16海里/时的速度从A港向东北方向航行，另一艘船同时以12海里/时的速度从A港向西北方向航行，经过 $1.5$ 小时后，它们相距海里．

查看试题解析
11. 在 $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别是a、b、c，满足 $(a - b)^{2} + | a^{2} + b^{2} - c^{2} | = 0$ ，则 $△ A B C$ 是三角形．

查看试题解析
12. 如图，四边形 $O A B C$ 是一张放在平面直角坐标系中的正方形纸片，点O与坐标原点重合，点A在x轴上，点C在y轴上， $O C = 5$ ，点E在边 $B C$ 上，点N的坐标为 $(3 ， 0)$ ，过点N且平行于y轴的直线 $M N$ 与 $E B$ 交于点M.现将纸片折叠，使顶点C落在 $M N$ 上的点G处，折痕为 $O E$ ．在x轴正半轴上存在一点P，使得以P，O，G为顶点的三角形为等腰三角形，则点P的坐标为．

查看试题解析

三、解答题

13. 计算：

(1)、 $\sqrt{20} + \sqrt{45} - \sqrt{8} + 4 \sqrt{2}$

(2)、 $| 1 - \sqrt{3} | + \sqrt{\frac{1}{3}} - \sqrt[3]{27} - (- 4)$ ．

查看试题解析
14. 已知2a﹣1的平方根为±3，3a+b﹣1的算术平方根为4，求a+2b的平方根．

查看试题解析
15. 在平面直角坐标系中，有 $A (- 2, a + 2)$ ， $B (a - 3, 4)$ ， $C (b - 4, b)$ 三点．

(1)、当 $A B ∥ x$ 轴时，求A、B两点间的距离；

(2)、当 $C D ⊥ x$ 轴于点D ，且 $C D = 3$ 时，求点C的坐标．

查看试题解析
16. 如图①、如图②、如图③均为 $3 \times 5$ 的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，按下列要求作图：

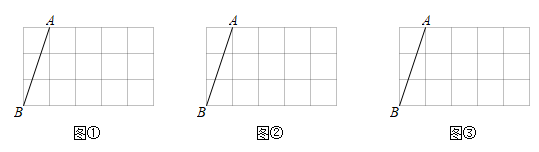(1)、在如图①中画出 $R t △ A B C$ ，使三个顶点均在格点上且 $A C = A B$ ， $∠ B A C = 90 °$ ；

(2)、在如图②中画出 $R t △ A B C$ ，使三个顶点均在格点上且 $A C = B C$ ， $∠ A C B = 90 °$ ；

(3)、在如图③中画出 $△ A B C$ ，使三个顶点均在格点上且 $A C = B C$ ， $∠ A C B \neq 90 °$ ．

查看试题解析
17. 如图，在平面直角坐标系中，直线 $y = k x + 4$ 经过点 $B (- 6 ， 0)$ 和点 $C (m ， 2)$ ，与y轴交于点A，经过点C的另一直线与y轴的正半轴交于点 $D (0 ， 1)$ ，与x轴交于点E．

(1)、求点A的坐标及直线 $C D$ 的解析式；

(2)、求四边形 $O B C D$ 的面积．

查看试题解析
18. 图1是超市购物车，图2为超市购物车侧面示意图，测得∠ACB=90°，支架AC=4.8dm，CB=3.6dm．

(1)、两轮中心 $A B$ 之间的距离为dm；

(2)、若 $O F$ 的长度为 $\sqrt{50}$ dm，支点F到底部 $D O$ 的距离为5dm，试求 $∠ F O D$ 的度数．

查看试题解析
19. 2022年在北京举行的第 $24$ 届冬奥会吉祥物“冰墩墩”和第 $13$ 届冬残奥会吉祥物“雪容融”备受广大人民的喜爱，一时掀起了追捧吉祥物的热潮．某商店为了满足广大人民的需要，预计购进两种吉祥物 $100$ 个．根据要求，“冰墩墩”的数量要多于“雪容融”的数量，且“冰墩墩”的数量不能超过 $53$ 个．设全部售出后的总利润为y元，购进“冰墩墩”x个．两种吉祥物的成本和售价如表：
类别
冰墩墩
雪容融
成本（元/个）
$48$
$40$
售价（元/个）
$56$
$46$

(1)、求y与x的函数关系式；

(2)、求该商店本次购买两种吉祥物共有几种方案？哪种方案的总利润最大？

查看试题解析
20. 小明在做二次根式的化简时，遇到了比较复杂的二次根式 $\sqrt{5 - 2 \sqrt{6}}$ ，通过资料的查询，他得到了该二次根式的化简过程如下
$\sqrt{5 - 2 \sqrt{6}} = \sqrt{2 - 2 \times \sqrt{2} \times \sqrt{3} + 3}$
＝ $\sqrt{{(\sqrt{2})}^{2} - 2 \times \sqrt{2} \times \sqrt{3} + {(\sqrt{3})}^{2}}$
＝ $\sqrt{{(\sqrt{2} - \sqrt{3})}^{2}}$
$= | \sqrt{2} - \sqrt{3} |$
= $\sqrt{3} - \sqrt{2}$

(1)、结合以上化简过程，请你动手尝试化简 $\sqrt{4 - 2 \sqrt{3}}$ ．

(2)、善于动脑的小明继续探究：当a，b，m，n为正整数时，若 $a + 2 \sqrt{b} =$ ${(\sqrt{m} + \sqrt{n})}^{2}$ ，则 $a + 2 \sqrt{b} = (m + n) + 2 \sqrt{m n}$ ，所以 $a = m + n ， b = m n$ ，若 $a + 2 \sqrt{17} =$ ${(\sqrt{m} + \sqrt{n})}^{2}$ ，且a，m，n为正整数， $m > n$ ；求a，m，n的值．

查看试题解析
21. 如图1，将射线 $O X$ 按逆时针方向旋转β角，得到射线 $O Y$ ，如果点P为射线 $O Y$ 上的一点，且 $O P = a ，$ ，那么我们规定用 $(a ， β)$ 表示点P在平面内的位置，并记为 $P (a ， β)$ ，例如，图2中，如果 $O M = 8$ ， $∠ X O M = 110 °$ ，那么点M在平面内的位置，记为 $M (8 ， 110)$ ，根据图形，解答下面的问题：

(1)、如图3，如果点N在平面内的位置记为 $N (6 ， 30)$ ，那么 $O N =$ ； $∠ X O N =$ ．

(2)、如果点A、B在平面内的位置分别记为 $A (5 ， 30) ， B (12 ， 120)$ ，试求A、B两点之间的距离并画出图．

查看试题解析
22. 我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列两个问题：

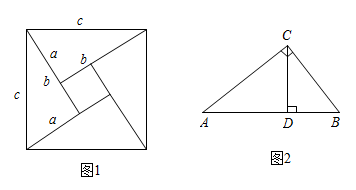(1)、如图 $①$ 是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理 $；$

(2)、如图 $②$ ，在 $R t △ A B C$ 中， $∠ A C B = 9 0^{∘}$ ， $C D$ 是 $A B$ 边上的高， $A C = 4$ ， $B C = 3$ ，求 $C D$ 的长度 $；$

(3)、如图①，若大正方形的面积是 $13$ ，小正方形的面积是 $1$ ，求 ${(a + b)}^{2}$ 的值．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 5 c m$ ， $B C = 3 c m ．$ 若点P从点A出发，以 $2 c m / s$ 的速度沿折线 $A - C - B$ 向点B运动，设运动时间为 $t 秒$ （ $t > 0$ ）．

(1)、在 $A C$ 上是否存在点P，使得 $P A = P B ？$ 若存在，求出t的值；若不存在，请说明理由．

(2)、若点P在运动的过程中，与三角形另一顶点的连线恰好平分 $△ A B C$ 的面积，求出t的值．

(3)、若点P恰好在 $△ A B C$ 的角平分线上（顶点除外），请直接写出 $t$ 的值 $．$

查看试题解析

类别	冰墩墩	雪容融
成本（元/个）	$48$	$40$
售价（元/个）	$56$	$46$