广东省中山市开发区2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-11-24 类型：期中考试
一、单选题
-
1. 下面四个图形分别是绿色食品、低碳、节能和节水标志，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组长度的三条线段能组成三角形的是（ ）A、 ， ， B、 ， ， C、 ， ， D、 ， ，3. 若一个正多边形的一个外角为36°，则这个图形为正（ ）边形．A、八 B、九 C、十 D、十一4. 在如图的△ABC中，正确画出AC边上的高的图形是（ ）A、
B、
C、
D、
5. 下列生活中的一些事实运用了“三角形稳定性”的是（ ）A、
B、
C、
D、
6. 一个三角形的三边长分别为2，5，x，另一个三角形的三边长分别为y，2，6，若这两个三角形全等，则x+y=（ ）A、11 B、7 C、8 D、137. 如图，要测池塘两端A，B的距离，小明先在地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB，发现DE＝AB．那么判定△ABC和△DEC全等的依据是（ ）
A、SSS B、SAS C、ASA D、AAS8. 如图，在△ABC中，已知∠B＝∠C＝50°，AD是△ABC的中线，则∠BAD的度数是（ ）
A、40° B、30° C、35° D、50°9. 如图，△ABC沿直线MN折叠，使点A与AB边上的点E重合，若∠B=54°，∠C=90°，则∠ENC等于（ ）
A、54° B、62° C、72° D、76°10. 如图，是的中线，E，F分别是和延长线上的点，且 ， 连接 ， 下列说法：①和面积相等；②；③；④；⑤ ． 其中正确的是（ ）
A、①② B、③⑤ C、①③④ D、①④⑤二、填空题
-
11. 等腰三角形的两边长分别是4和8 ， 则它的周长是 ．12. 在平面直角坐标系中，若点与点关于y轴对称，则 ．13. 如图△ABC中，AD是BC上的中线，BE是△ABD中AD边上的中线，若△ABC的面积是12，则△ABE的面积是 ．
14. 如图中， ， 以顶点A为圆心，任意长为半径画弧，分别交、于点M、N，再分别以点M、N为圆心，大于的长为半径画弧，两弧交于点P，作射线交边于点D，若 ， ， 则的面积是 ．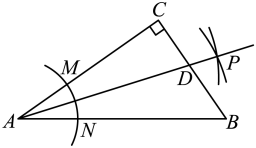
15. 如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝5，线段PQ＝AB，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP＝时，△ABC≌△QPA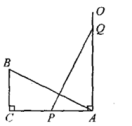
三、解答题
-
16. 一个多边形，它的内角和比外角和的 倍多 求这个多边形的边数.17. 如图，在等腰中， ， 是边上的中线， ， 求证： ．
18. 如图，AB=DE，AC=DF，BE=CF．求证：AB∥DE．
19. 如图，在△ABC中，∠A＞∠B．
(1)、作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）．(2)、在（1）的条件下，连接AE，若∠B＝45°，求∠AEC的度数．20. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-3，5），B（-4，3），C（-1，1）.
(1)、画出△ABC关于x轴对称的△A1B1C1；并填写出△A1B1C三个顶点的坐标.A1 （ ， ）；
B1 （ ， ）；
C1 （ ， ）.
(2)、求△ABC的面积.21. 数学活动：利用全等三角形研究“筝形”的特征．认识图形：如图，四边形中， ． 像这样，两条邻边分别相等的四边形叫做筝形．
(1)、研究特征：小明猜想筝形的对角与相等，他的结论成立吗？说明理由；(2)、研究特征：小梅连接筝形的后发现垂直平分 ， 请你补全图形，并帮她说明理由．
