广东省阳江市江城区2022-2023学年八年级上学期期中考试数学试题
试卷更新日期:2022-11-24 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,工人师傅砌门时,常用木条EF固定矩形门框ABCD,使其不变形,这种做法的根据是( )
2. 如图,工人师傅砌门时,常用木条EF固定矩形门框ABCD,使其不变形,这种做法的根据是( )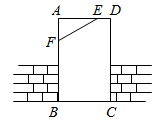 A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 图中能表示 的BC边上的高的是A、
A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 图中能表示 的BC边上的高的是A、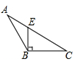 B、
B、 C、
C、 D、
D、 4. 每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm5. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
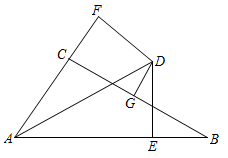
4. 每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm5. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( ) A、SSS B、SAS C、ASA D、AAS6. 在三角形内部,到三角形三边距离相等的点是( )A、三条中线的交点 B、三条高线交点 C、三边垂直平分线交点 D、三个内角平分线交点7. 如图, , 若 , , 则的度数为( )
A、SSS B、SAS C、ASA D、AAS6. 在三角形内部,到三角形三边距离相等的点是( )A、三条中线的交点 B、三条高线交点 C、三边垂直平分线交点 D、三个内角平分线交点7. 如图, , 若 , , 则的度数为( ) A、 B、 C、 D、8. 如图,已知△ABC的面积为24,AB=AC=8,点D为BC边上一点,过点D分别作DE⊥AB于E,DF⊥AC于F,若DF=2DE,则DF长为( )
A、 B、 C、 D、8. 如图,已知△ABC的面积为24,AB=AC=8,点D为BC边上一点,过点D分别作DE⊥AB于E,DF⊥AC于F,若DF=2DE,则DF长为( ) A、4 B、5 C、6 D、89. 在ABC和中,已知∠A=∠ , AB= , 添加下列条件中的一个,不能使ABC≌一定成立的是( )A、AC= B、BC= C、∠B=∠ D、∠C=∠10. 如图,在已知的中,按以下步骤作图:
A、4 B、5 C、6 D、89. 在ABC和中,已知∠A=∠ , AB= , 添加下列条件中的一个,不能使ABC≌一定成立的是( )A、AC= B、BC= C、∠B=∠ D、∠C=∠10. 如图,在已知的中,按以下步骤作图:
①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线交于点D,连接 .
若 , , 则的周长为( )
A、8 B、9 C、10 D、14二、填空题
-
11. 若点P(a-2,3)与Q(1,b+1)关于x轴对称,则a+b= .12. 一个多边形的每个内角都是150°,那么这个多边形的边数为 .13. 如图, , , , 则°.
 14. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC面积等于4 , 则△BEF的面积等于 .
14. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC面积等于4 , 则△BEF的面积等于 . 15. 如图,将△ABC沿着平行于BC的直线折叠,点A落在点A′,若∠C=125°,∠A=15°,则∠A′DB的度数为 .
15. 如图,将△ABC沿着平行于BC的直线折叠,点A落在点A′,若∠C=125°,∠A=15°,则∠A′DB的度数为 .
三、解答题
-
16. 一个正多边形的每个内角都是相邻外角的3倍,则这个正多边形是几边形?每个内角是多少度?17. 如图,在中,是上一点,E是上一点,与相交于点O, , , , 求和的度数.
 18. 如图,已知AB∥DE,AB = DE,B,E,C,F在同一条直线上,且BE = CF.
18. 如图,已知AB∥DE,AB = DE,B,E,C,F在同一条直线上,且BE = CF.求证∶△ABC≌△DEF.
 19. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.
19. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上. (1)、作出关于y轴对称的;(2)、写出点关于x轴对称的点的坐标;(3)、求的面积.20. 如图,在中,D是边上的一点, , 平分 , 交边于点E,连接 .
(1)、作出关于y轴对称的;(2)、写出点关于x轴对称的点的坐标;(3)、求的面积.20. 如图,在中,D是边上的一点, , 平分 , 交边于点E,连接 . (1)、求证:;(2)、若 , , 求的度数.21. 如图,四边形ABCD中,BC=CD=2AB,ABCD,∠B=90°,E是BC的中点,AC与DE相交于点F.
(1)、求证:;(2)、若 , , 求的度数.21. 如图,四边形ABCD中,BC=CD=2AB,ABCD,∠B=90°,E是BC的中点,AC与DE相交于点F. (1)、求证:ABC≌ECD;(2)、判断线段AC与DE的位置关系,并说明理由.
(1)、求证:ABC≌ECD;(2)、判断线段AC与DE的位置关系,并说明理由.