广东省广州市祈福教育集团2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-11-24 类型:期中考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,不能看作是轴对称图形的是( )A、迎 B、二 C、十 D、大2. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
 A、SSS B、SAS C、ASA D、AAS3. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A、SSS B、SAS C、ASA D、AAS3. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )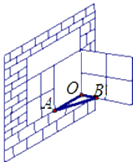 A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短4. 如图,若△ABC≌△DEF,四个点B、E、C、F在同一直线上,BC=7,EC=5,则CF的长是( )
A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短4. 如图,若△ABC≌△DEF,四个点B、E、C、F在同一直线上,BC=7,EC=5,则CF的长是( )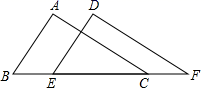 A、2 B、3 C、5 D、75. 一个多边形的内角和与外角和之比为 , 则这个多边形的边数是( )A、7 B、8 C、9 D、106. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2 , AB=13cm,AC=7cm,则DE的长( )
A、2 B、3 C、5 D、75. 一个多边形的内角和与外角和之比为 , 则这个多边形的边数是( )A、7 B、8 C、9 D、106. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2 , AB=13cm,AC=7cm,则DE的长( ) A、3cm B、4cm C、5cm D、6cm7. 如图,已知 , , , 则等于( )
A、3cm B、4cm C、5cm D、6cm7. 如图,已知 , , , 则等于( ) A、 B、 C、 D、8. 如图,在中,点D,E分别在边上,将沿折叠至位置,点A的对应点为F.若 , 则的度数为( )
A、 B、 C、 D、8. 如图,在中,点D,E分别在边上,将沿折叠至位置,点A的对应点为F.若 , 则的度数为( )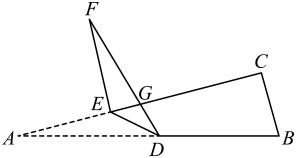 A、 B、 C、 D、9. 如图,△ABC的三边长均为整数,且周长为22,AM是边BC上的中线,△ABM的周长比△ACM的周长大2,则BC长的可能值有( )个.
A、 B、 C、 D、9. 如图,△ABC的三边长均为整数,且周长为22,AM是边BC上的中线,△ABM的周长比△ACM的周长大2,则BC长的可能值有( )个. A、4 B、5 C、6 D、710. 已知:如图,中,为的角平分线,且 , E为延长线上的一点, , 过E作 , F为垂足.下列结论:①;②;③;④ . 其中正确的个数是( )
A、4 B、5 C、6 D、710. 已知:如图,中,为的角平分线,且 , E为延长线上的一点, , 过E作 , F为垂足.下列结论:①;②;③;④ . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知∠CDE=90°,∠CAD=90°,BE⊥AD于B,且DC=DE,若BE=7,AB=4,则BD的长为 .
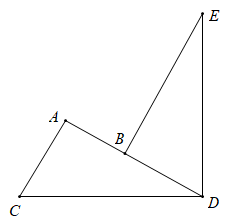 12. 等腰三角形中, , , 则的长为 .13. 如图,小明从A点出发,前进6m到点B处后向右转 , 再前进6m到点C处后又向右转 , …,这样一直走下去,他第一次回到出发点A时,一共走了 m.
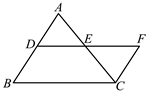
12. 等腰三角形中, , , 则的长为 .13. 如图,小明从A点出发,前进6m到点B处后向右转 , 再前进6m到点C处后又向右转 , …,这样一直走下去,他第一次回到出发点A时,一共走了 m.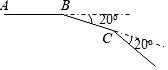 14. 如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2 , 则图中阴影部分△BEF的面积等于cm2 .
14. 如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2 , 则图中阴影部分△BEF的面积等于cm2 . 15. 如图,线段的垂直平分线、相交于点O,若 , 则的度数是 .
15. 如图,线段的垂直平分线、相交于点O,若 , 则的度数是 . 16. 如图,中, , 直线l经过点C且与边相交.动点P从点A出发沿路径向终点B运动;动点Q从点B出发沿路径向终点A运动.点P和点Q的速度分别为和 , 两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作于点E,于点F,设运动时间为t秒,则当t=秒时,与全等.
16. 如图,中, , 直线l经过点C且与边相交.动点P从点A出发沿路径向终点B运动;动点Q从点B出发沿路径向终点A运动.点P和点Q的速度分别为和 , 两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作于点E,于点F,设运动时间为t秒,则当t=秒时,与全等.
三、解答题
-
17. 已知,如图,D是△ABC的边AB上一点,DF交AC于点E,DE = FE,AB∥FC.
求证:AD = CF.
 18. 如图,两条公路 , 相交于点O,在内部有两个村庄C,D.为方便群众接种新冠疫苗,该地决定在内部再启动一个方舱式接种点P,要求同时满足:
18. 如图,两条公路 , 相交于点O,在内部有两个村庄C,D.为方便群众接种新冠疫苗,该地决定在内部再启动一个方舱式接种点P,要求同时满足: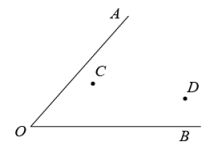
⑴到两条公路 , 的距离相等.
⑵到两村庄C,D的距离相等.请你用直尺和圆规作出接种点P的位置(保留作图痕迹).
19. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-1,1)、B(1,5)、C(4,4). (1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出顶点的坐标.(2)、求△A1B1C1的面积.20. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数。
(1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出顶点的坐标.(2)、求△A1B1C1的面积.20. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数。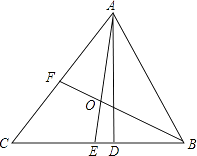 21. 如图在四边形中,平分 , 且与的角平分线交于点D,若 , , 求的度数.
21. 如图在四边形中,平分 , 且与的角平分线交于点D,若 , , 求的度数. 22. 如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
22. 如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB. (1)、求∠BPC的度数;(2)、连接EF,求证:△EFP是等腰三角形.23. 等边 , D为外一点, , 射线与直线相交于点M,射线与直线相交于点N.
(1)、求∠BPC的度数;(2)、连接EF,求证:△EFP是等腰三角形.23. 等边 , D为外一点, , 射线与直线相交于点M,射线与直线相交于点N. (1)、当点M、N在边上,且时,猜想之间的数量关系,并且请证明.(2)、当点M、N在边的延长线上时,请画出图形,并写出之间的数量关系.24. 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
(1)、当点M、N在边上,且时,猜想之间的数量关系,并且请证明.(2)、当点M、N在边的延长线上时,请画出图形,并写出之间的数量关系.24. 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. (1)、求证:△ADC≌△AEB;(2)、判断△EGM是什么三角形,并证明你的结论;(3)、判断线段BG、AF与FG的数量关系并证明你的结论.25. 如图,在平面直角坐标系中,已知A(0,a)、B(-b,0)且a、b满足+|a-2b+2|=0
(1)、求证:△ADC≌△AEB;(2)、判断△EGM是什么三角形,并证明你的结论;(3)、判断线段BG、AF与FG的数量关系并证明你的结论.25. 如图,在平面直角坐标系中,已知A(0,a)、B(-b,0)且a、b满足+|a-2b+2|=0 (1)、求证:∠OAB=∠OBA;(2)、如图1,若BE⊥AE,求∠AEO的度数;(3)、如图2,若D是AO的中点,DEBO,F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量和位置关系.
(1)、求证:∠OAB=∠OBA;(2)、如图1,若BE⊥AE,求∠AEO的度数;(3)、如图2,若D是AO的中点,DEBO,F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量和位置关系.