广东省佛山市南海区狮山镇2022-2023学年八年级上学期期中考试数学试题

试卷更新日期：2022-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 根据下列表述，能够确定具体位置的是（）

A、北偏东25°方向 B、距学校800米处 C、温州大剧院音乐厅8排 D、东经20°北纬30°

查看试题解析
2. 在平面直角坐标系中，点 $P (- 1 ， - 2)$ 关于x轴对称的点的坐标是（）

A、 $(1 ， - 2)$ B、 $(1 ， 2)$ C、 $(- 1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 如图，三个正方形围成一个直角三角形，图中的数据是它们的面积，则正方形A的面积为（）

A、9 B、16 C、25 D、5

查看试题解析
4. 如图是汽车加完汽油后，加油机显示屏上显示的内容．在加油过程中加油机显示屏上的三个量中，常量是（）

A、金额 B、数量 C、单价 D、金额和数量

查看试题解析
5. 下列数是无理数的是（）

A、 $\frac{1}{3}$ B、 $π$ C、 $0 . \overset{\cdot}{6} \overset{\cdot}{3}$ D、3.1415

查看试题解析
6. 3的平方根是（）

A、 9 B、 $\sqrt{3}$ C、 $- \sqrt{3}$ D、 $\pm \sqrt{3}$

查看试题解析
7. 下列4组数据中，是勾股数的是（　　）

A、1，2，3 B、2，3，4 C、3，4，5 D、6，7，8

查看试题解析
8. 已知x为实数，且 $\sqrt{x + 2} = 0$ ，则x的值为（）

A、 $- 2$ B、 $- 8$ C、2 D、8

查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $2 \sqrt{3} - 2 = \sqrt{3}$ D、 $2 \sqrt{3} - \sqrt{3} = 2$

查看试题解析
10. 若 $k > 0$ ， $b > 0$ ，则函数 $y = k x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

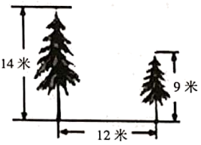
11. 比较大小：4 $\sqrt{17}$ （填“>”“<”或“=”）.

查看试题解析
12. 如果某数的一个平方根是﹣2，那么这个数是.

查看试题解析
13. 若点A的坐标是 $(- 2 ， 3)$ ，则它到y轴的距离是．

查看试题解析
14. 如图，在校园内有两棵树相距12米，一棵树高14米，另一棵树高9米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞米．

查看试题解析
15. 如图，直线 $l_{1} ⊥ x$ 轴于点 $(1 ， 0)$ ，直线 $l_{2} ⊥ x$ 轴于点 $(2 ， 0)$ ，直线 $l_{3} ⊥ x$ 轴于点 $(3 ， 0)$ ， …直线 $l_{n} ⊥ x$ 轴于点 $(n ， 0)$ ．函数 $y = x$ 的图象与直线l₁ ， l₂ ， l₃ ， ……ln分别交于点A₁ ， A₂ ， A₃ ， ……An；函数y＝3x的图象与直线l₁ ， l₂ ， l₃ ， ……ln分别交于点B₁ ， B₂ ， B₃ ， ……Bn，如果 $△ O A_{1} B_{1}$ 的面积记的作 $S_{1}$ ，四边形 $A_{1} A_{2} B_{2} B_{1}$ 的面积记作 $S_{2}$ ，四边形 $A_{2} A_{3} B_{3} B_{2}$ 的面积记作 $S_{3}$ ， …四边形 $A_{n - 1} A_{n} B_{n} {B_{n}}_{- 1}$ 的面积记作 $S_{n}$ ，那么 $S_{2020} =$ ．

查看试题解析

三、解答题

16. 计算： $2 \sqrt{12} \times \frac{\sqrt{3}}{4} + \sqrt{24} \div \sqrt{6}$

查看试题解析
17. 已知y关于x成正比例，且当x＝2时，y＝-6，求：当x＝1时，y的值．

查看试题解析
18. 请在数轴上用尺规作出 $\sqrt{2}$ 所对应的点．（要求保留作图痕迹）

查看试题解析
19. 如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
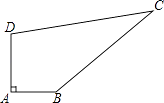20. 如图所示，有一个圆柱，它的高为9厘米，底面周长为24厘米，在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物，问它爬行的最短路程是多少厘米？

查看试题解析
21. 如图所示在直角坐标系中，每个小正方形的边长为1， $△ A B C$ 的顶点格点都落在网格线的交点上

(1)、请作出将 $△ A B C$ 向下平移3个单位长度，再向右平移2个单位长度后的 $△ A^{'} B^{'} C^{'}$ ；并写出三个顶点的坐标．

(2)、求三角形 $△ A^{'} B^{'} C^{'}$ 的面积

查看试题解析
22. 阅读以下材料：将分母中的根号化去，叫做分母有理化．分母有理化的方法，一般是把分子分母都乘以同一个适当的代数式，使分母不含根号．例如： $\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{(\sqrt{2})^{2}} = \frac{\sqrt{2}}{2}$ ，

(1)、将 $\frac{1}{\sqrt{2} + 1}$ 分母有理化可得；

(2)、求 $\frac{1}{1 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{5}} + \frac{1}{\sqrt{5} + \sqrt{7}} + \cdot \cdot \cdot + \frac{1}{\sqrt{97} + \sqrt{99}}$ 的值．

查看试题解析

23. 对于函数

y = | x | + b

，小明探究了它的图象及部分性质．下面是他的探究过程，请补充完整：

(1)、自变量x的取值范围是；

(2)、令b分别取0，1和-2，所得三个函数中的自变量与其对应的函数值如下表，则表中m的值是， n的值是；

$x$	…	$- 3$	$- 2$	$- 1$	0	1	2	3	…
$y = \| x \|$	…	3	2	1	0	1	2	3	…
$y = \| x \| + 1$	…	4	$m$	2	1	2	3	4	…
$y = \| x \| - 2$	…	1	0	$n$	$- 2$	$- 1$	0	1	…

(3)、根据表中数据，补全函数

y = | x |

，

y = | x | + 1

，

y = | x | - 2

的图象：

(4)、结合函数

y = | x |

，

y = | x | + 1

，

y = | x | - 2

的图象，写出函数

y = | x | + b

的一条性质：；

(5)、点

(x_{1} ， y_{1})

和点

(x_{2} ， y_{2})

都在函数

y = | x | + b

的图象上，当

x_{1} x_{2} > 0

时，若总有

y_{1} < y_{2}

，结合函数图象，直接写出

x_{1}

和

x_{2}

的大小关系．

查看试题解析