安徽省皖东南三校2022-2023学年八年级上学期联考数学期中试题

试卷更新日期：2022-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系的第四象限内有一点M，到x轴的距离为4，到y轴的距离为5，则点M的坐标为（）

A、 $(- 4 ， 5)$ B、 $(- 5 ， 4)$ C、 $(4 ， - 5)$ D、 $(5 ， - 4)$

查看试题解析
2. 若a、b、c为△ABC的三边长，且满足|a﹣4|+ $\sqrt{b - 2}$ =0，则c的值可以为（）

A、5 B、6 C、7 D、8

查看试题解析
3. 函数 $y = \frac{x}{\sqrt{x + 3}} + \frac{1}{x - 1}$ 的自变量x的取值范围是（）

A、 $x \neq - 3$ 且 $x \neq 1$ B、 $x > - 3$ 且 $x \neq 1$ C、 $x > - 3$ D、 $x \geq - 3$ 且 $x \neq 1$

查看试题解析
4. 在△ABC中，∠A＝20°，∠B＝4∠C，则∠C等于（）

A、32° B、36° C、40° D、128°

查看试题解析
5. 在直角坐标系中，点M，N在同一个正比例函数图象上的是（　　）

A、M（2，﹣3），N（﹣4，6） B、M（﹣2，3），N（4，6） C、M（﹣2，﹣3），N（4，﹣6） D、M（2，3），N（﹣4，6）

查看试题解析
6. 设一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $(1 ， - 3)$ ，且y的值随x的值增大而增大，则该一次函数的图象一定不经过 $($ 　　 $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 将直线 $y = 2 x - 3$ 向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（）

A、 $y = 2 x - 4$ B、 $y = 2 x + 4$ C、 $y = 2 x + 2$ D、 $y = 2 x - 2$

查看试题解析
8. 小明和小华是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公交汽车到了学校．如图是他们从家到学校已走的路程s（米）和所用时间t（分钟）的关系图．则下列说法中错误的是（）

A、小明吃早餐用时5分钟 B、小华到学校的平均速度是240米/分 C、小明跑步的平均速度是100米/分 D、小华到学校的时间是7：55

查看试题解析
9. 已知一次函数 $y = k x + b$ 的图象经过点 $(- 2 ， 1)$ ，且平行于直线 $y = - 2 x$ ，则b的值为（）

A、 $- 2$ B、1 C、 $- 3$ D、4

查看试题解析
10. 当－1≤x≤2时，函数y＝ax＋6满足y＜10，则常数a的取值范围（）

A、－4＜a＜0 B、0＜a＜2 C、－4＜a＜2且a≠0 D、－4＜a＜2

查看试题解析

二、填空题

11. 若 $y = (k - 3) x^{| k | - 2} + 5$ 是一次函数，则k＝．

查看试题解析
12. 函数 $y = \frac{x - 2}{3}$ 的图象在y轴的截距是．

查看试题解析
13. 已知a、b、c是 $△ A B C$ 的三边，则化简 $| a + b - c | + | b - c - a | - | c - a + b |$ 的结果是．

查看试题解析
14. 自变量x与因变量y的关系式为： $y = 2 x + 5$ ，当x每增加1时，y增加．

查看试题解析
15. 已知直线y=x+b和y=ax+2交于点P（3，-1），则关于x的方程（a-1）x=b-2的解为．

查看试题解析
16. 如图，在 $△ A B C$ 中，点D是 $B C$ 的中点，点E是 $A C$ 上一点， $E C = 2 A E$ ， $A D = 2 A F$ ，已知 $△ A B C$ 的面积为30，那么四边形 $C D F E$ 的面积为．

查看试题解析

三、解答题

17. 如图，在边长为 $1$ 个单位长度的小正方形网格中建立平面直角坐标系 $.$ 已知三角形 $A B C$ 的顶点A的坐标为 $A (- 1 ， 4)$ ，顶点B的坐标为 $(- 4 ， 3)$ ，顶点C的坐标为 $(- 3 ， 1)$ ．

(1)、把三角形 $A B C$ 向右平移5个单位长度，再向下平移4个单位长度得到三角形 $A^{'} B^{'} C^{'}$ ，请你画出三角形 $A^{'} B^{'} C^{'}$ ；

(2)、请直接写出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(3)、求三角形 $A B C$ 的面积．

查看试题解析
18. 已知 $y = y_{1} + y_{2}$ ，且 $y_{1} - 3$ 与x成正比例， $y_{2}$ 与 $x - 2$ 成正比例，当 $x = 2$ 时， $y = 7$ ，当 $x = 1$ 时， $y = 0$ ．

(1)、求出y与x之间的函数关系式；

(2)、计算 $x = 4$ 时，y的值．

查看试题解析
19. 如图，函数 $y = - 2 x + 3$ 与 $y = - \frac{1}{2} x + m$ 的图象交于 $P (n ， - 2)$ ，直线 $y = - 2 x + 3$ 与y轴交于点A，直线 $y = - \frac{1}{2} x + m$ 与y轴交于点B．

(1)、求出m，n的值；

(2)、直接写出不等式 $- \frac{1}{2} x + m > - 2 x + 3$ 的解集；

(3)、求出 $△ A B P$ 的面积．

查看试题解析
20. 如图，已知： $A D$ 平分 $∠ B A C$ ，点F是 $A D$ 反向延长线上的一点， $E F ⊥ B C$ ， $∠ 1 = 40 ° ， ∠ C = 65 °$ ．求： $∠ B$ 和 $∠ F$ 的度数．

查看试题解析
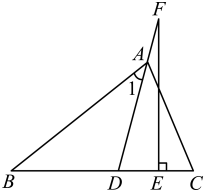21. 当前，新冠肺炎疫情仍在全球蔓延，国内疫情也呈现多地散发、部分聚集态势，接种新冠疫苗是构筑全民免疫的有力屏障，重庆市八月启动 $12 - 17$ 岁学生新冠病毒疫苗接种工作，小南和小开计划在父母陪同下前往医院接种新冠疫苗，小南从 $A$ 小区匀速步行前往 $B$ 医院接种，同时，小开留观结束从 $B$ 医院返回 $A$ 小区，两人之间的距离 $y$ （m）与步行时间 $x$ （min）的关系如图所示．

(1)、 $A$ 小区和 $B$ 医院的距离为m，小南和小开出发min后相遇；

(2)、若小南的步行速度比小开的步行速度快；求小南和小开步行的速度各是多少？

(3)、计算出点 $C$ 对应的步行时间 $x$ 和两人之间的距离 $y$ ，并解释点 $C$ 的实际意义．

查看试题解析
22. 某商业集团准备购进A，B两款口袋打印机在甲、乙两个商场进行销售，这两款口袋打印机每台的利润如表：
打印机利润商场
甲商场
乙商场
A款（元/台）
95
60
$B$ 款（元/台）
70
45
为迎接双十二，该商业集团新进了40台A款，60台B款调配给甲，乙两个商场，其中70台给甲商场，30台给乙商场．

(1)、设该集团调配给甲商场A款x台，求总利润y与x的函数关系式．

(2)、①若这100台口袋打印机全部销售出去，如何调配才能让商业集团的利润最大，并求出利润的最大值．
②为了促销，该商业集团决定对甲商场的A款，B款每台分别让利a元和b元（ $5 \leq b \leq 8$ ），其他销售利润不变，当天结算时发现销售总利润与调配方案无关．当总利润最大时，求此时a的值．

查看试题解析

打印机利润商场	甲商场	乙商场
A款（元/台）	95	60
$B$ 款（元/台）	70	45