山东省淄博市张店区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-24 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、 B、 C、 D、2. 下列疫情防控宣传图片中,是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 3. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
3. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )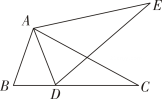 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED4. 如图,用尺规作 的依据是( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED4. 如图,用尺规作 的依据是( )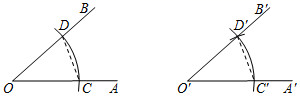 A、SAS B、ASA C、AAS D、SSS5. △ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( )
A、SAS B、ASA C、AAS D、SSS5. △ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( ) A、5° B、10° C、12° D、20°6. 如图,是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为(-3,1),棋子“炮”的坐标为(1,1),则棋子“马”的坐标为( )
A、5° B、10° C、12° D、20°6. 如图,是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为(-3,1),棋子“炮”的坐标为(1,1),则棋子“马”的坐标为( ) A、(3,-1) B、(2,-2) C、(2,-1) D、(2,0)7. 如图,BD是△ABC的中线,点E,F分别为BD,CE的中点,若△ABC的面积为8.则△AEF的面积是( )
A、(3,-1) B、(2,-2) C、(2,-1) D、(2,0)7. 如图,BD是△ABC的中线,点E,F分别为BD,CE的中点,若△ABC的面积为8.则△AEF的面积是( ) A、2 B、3 C、4 D、68. 介于两个连续(相邻)的整数a与b之间,则a+b=( )A、1 B、3 C、5 D、79. 如图,中, , , AD是BC上的高, , 图中与BD(BD除外)相等的线段共有( )条.
A、2 B、3 C、4 D、68. 介于两个连续(相邻)的整数a与b之间,则a+b=( )A、1 B、3 C、5 D、79. 如图,中, , , AD是BC上的高, , 图中与BD(BD除外)相等的线段共有( )条. A、1 B、2 C、3 D、410. 甲、乙两人沿同一条路从A地出发,去往100千米外的B地,甲、乙两人离A地的距离(千米)与时间t(小时)之间的关系如图所示,以下说法正确的是( )
A、1 B、2 C、3 D、410. 甲、乙两人沿同一条路从A地出发,去往100千米外的B地,甲、乙两人离A地的距离(千米)与时间t(小时)之间的关系如图所示,以下说法正确的是( ) A、甲出发2小时后两人第一次相遇 B、乙的速度是30km/h C、甲乙同时到达B地 D、甲的速度是60km/h11. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.若AB=7,AC=3,则BE=( )
A、甲出发2小时后两人第一次相遇 B、乙的速度是30km/h C、甲乙同时到达B地 D、甲的速度是60km/h11. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.若AB=7,AC=3,则BE=( ) A、1 B、2 C、3 D、412. 记实数x1 , x2 , …,xn中的最小数为min|x1 , x2 , …,xn|,例如min|-1,1,2|=-1,则函数y=min|2x-1,x,4-x|的图象大致为( )A、
A、1 B、2 C、3 D、412. 记实数x1 , x2 , …,xn中的最小数为min|x1 , x2 , …,xn|,例如min|-1,1,2|=-1,则函数y=min|2x-1,x,4-x|的图象大致为( )A、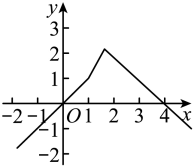 B、
B、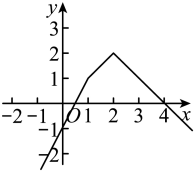 C、
C、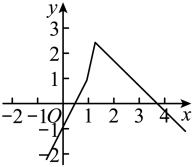 D、
D、
二、填空题
-
13. 计算: = .14. 已知点P(a,b)在第三象限,点P到x轴的距离为3,到y轴的距离为5,则点P的坐标为 .15. 甲,乙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,-2);
乙:y随x的增大而减小;
丙:函数的图象不经过第一象限.
根指他们的叙述,写出满足上述性质的一个一次函数的表达式为 .
16. 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 .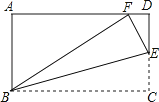 17. 如图,在平面直角坐标系中有两条直线l1: , l2: . 则AB与AC的数量关系为 , 若l2上的一点M到l1的距高是2.则点M的坐标为 .
17. 如图,在平面直角坐标系中有两条直线l1: , l2: . 则AB与AC的数量关系为 , 若l2上的一点M到l1的距高是2.则点M的坐标为 .
三、解答题
-
18.(1)、;(2)、求满足式子的未知数x: .19. 实数与数轴上的点一一对应,无理数也可以在数轴上表示出来,
 (1)、如图1,点A表示的数是;(2)、如图2,直线1垂直数轴于点B,点B对应的数是3,请在数轴上用尺规作出表示的点C(不写作法,保留作图痕迹),并说明理由.20. 在平而直角坐标系中,点A、点B、点C、点O都在山边长为1的小正方形组成网格的格点上,△ABC的位置如图所示.
(1)、如图1,点A表示的数是;(2)、如图2,直线1垂直数轴于点B,点B对应的数是3,请在数轴上用尺规作出表示的点C(不写作法,保留作图痕迹),并说明理由.20. 在平而直角坐标系中,点A、点B、点C、点O都在山边长为1的小正方形组成网格的格点上,△ABC的位置如图所示.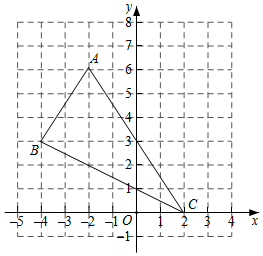 (1)、在上图中画由△ABC关于y轴对称的△A'B'C'.(2)、△ABC的顶点A关于y轴对称的点A'的坐标为:A';△A'B'C'的顶点B'关于x轴对称的点B'的坐标为B'';(3)、求△ABC的面积.21. 某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,收500元制版费:乙印刷厂提出:每份材料收0.4元印刷费,不收刺版费.
(1)、在上图中画由△ABC关于y轴对称的△A'B'C'.(2)、△ABC的顶点A关于y轴对称的点A'的坐标为:A';△A'B'C'的顶点B'关于x轴对称的点B'的坐标为B'';(3)、求△ABC的面积.21. 某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,收500元制版费:乙印刷厂提出:每份材料收0.4元印刷费,不收刺版费. (1)、分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;(2)、在如图所示的平面直角坐标系中画出这两个函数的图象;(3)、如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?(4)、旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?22. 课外兴趣小组活动时,老师提出了如下问题:
(1)、分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;(2)、在如图所示的平面直角坐标系中画出这两个函数的图象;(3)、如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?(4)、旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?22. 课外兴趣小组活动时,老师提出了如下问题: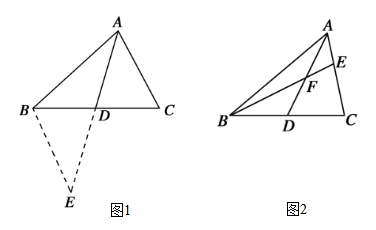 (1)、如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.(2)、如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.23. 如图,在平面直角坐标系中,过点A(0,8)的直线AB与直线OC相交于点C(2,6),与x轴交于点B,动点Q在直线AB上运动,动点P在直线OC上运动.
(1)、如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.(2)、如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.23. 如图,在平面直角坐标系中,过点A(0,8)的直线AB与直线OC相交于点C(2,6),与x轴交于点B,动点Q在直线AB上运动,动点P在直线OC上运动.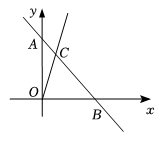 (1)、求直线AB和直线OC的表达式;(2)、当△OBQ的面积S△OBQ=12时,求此时点Q的坐标;(3)、是否存在点P,使△OBP是直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.24.
(1)、求直线AB和直线OC的表达式;(2)、当△OBQ的面积S△OBQ=12时,求此时点Q的坐标;(3)、是否存在点P,使△OBP是直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.24. (1)、问题背景:如图1,在四边形ABCD中AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法心,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(2)、探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,请说明现由;(3)、实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心北偏东60°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向南偏东75°方向以40海里/小时的速度前进,舰艇乙沿北偏西75°的方向以30海里/小时的速度前进,前进2小时后,指挥中心观察到甲、乙两舰艇分别到达E,F处,且E处在指挥中心北偏东8°方向,F处在指挥中心北偏东53°方向,试求此时两舰艇之间的距离.
(1)、问题背景:如图1,在四边形ABCD中AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法心,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(2)、探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,请说明现由;(3)、实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心北偏东60°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向南偏东75°方向以40海里/小时的速度前进,舰艇乙沿北偏西75°的方向以30海里/小时的速度前进,前进2小时后,指挥中心观察到甲、乙两舰艇分别到达E,F处,且E处在指挥中心北偏东8°方向,F处在指挥中心北偏东53°方向,试求此时两舰艇之间的距离.