山东省淄博市桓台县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-24 类型:期末考试
一、单选题
-
1. 已知三角形的两边长分别为2、10,则第三边长可能是( )A、6 B、8 C、10 D、122. 如图,已知 中, ,点 、 分别在 、 上, , ,则 等于( )
 A、 B、 C、 D、3. 点A(m+1,3m-7)在第一、三象限的角平分线上,则m的值为( )A、3 B、4 C、5 D、64. 如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,若AB=4,AC=5,则△ADE的周长为( )
A、 B、 C、 D、3. 点A(m+1,3m-7)在第一、三象限的角平分线上,则m的值为( )A、3 B、4 C、5 D、64. 如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,若AB=4,AC=5,则△ADE的周长为( ) A、8 B、9 C、10 D、135. 已知k<0,b<0,则一次函数y=kx+b的图象可能是( )A、
A、8 B、9 C、10 D、135. 已知k<0,b<0,则一次函数y=kx+b的图象可能是( )A、 B、
B、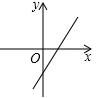 C、
C、 D、
D、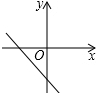 6. 如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1 , S2 , S3之间的关系为( )
6. 如图,Rt△ABC中,∠ACB=90°,图中三个正方形的面积S1 , S2 , S3之间的关系为( ) A、S1=S2+S3 B、S1+S3=S2 C、S1+S2=S3 D、S12+S22=S327. 下列说法中正确的是( )A、9的平方根是3 B、0的立方根是0 C、的平方根是±4 D、1的立方根是±18. 如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A、S1=S2+S3 B、S1+S3=S2 C、S1+S2=S3 D、S12+S22=S327. 下列说法中正确的是( )A、9的平方根是3 B、0的立方根是0 C、的平方根是±4 D、1的立方根是±18. 如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( ) A、1个 B、2个 C、3个 D、4个9. 如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A、1个 B、2个 C、3个 D、4个9. 如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( ) A、13 海里 B、16 海里 C、20 海里 D、26 海里10. 已知如图是函数 的图象,则函数 的大致图象是( )
A、13 海里 B、16 海里 C、20 海里 D、26 海里10. 已知如图是函数 的图象,则函数 的大致图象是( ) A、
A、 B、
B、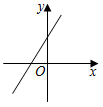 C、
C、 D、
D、 11. 按一定规律排列的一列数: , , , ,其中第6个数为( )A、 B、 C、 D、12. 如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止.已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )
11. 按一定规律排列的一列数: , , , ,其中第6个数为( )A、 B、 C、 D、12. 如图1,在长方形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止.已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则长方形ABCD的面积为( )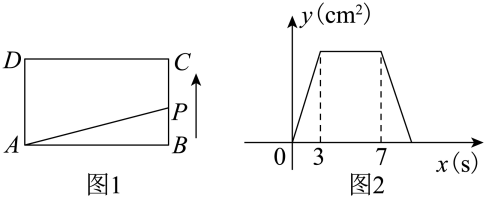 A、48cm2 B、24cm2 C、12cm2 D、6cm2
A、48cm2 B、24cm2 C、12cm2 D、6cm2二、填空题
-
13. 函数y=1-2x,y的值随着x的值的增大而 . (增大、减小、不变)14. 如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E,若AB=11cm,△BCE的周长为18cm,则BC=cm.
 15. 若(2x﹣5)2+ =0,则2x+4y的平方根是 .16. 如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4,则两条凳子的高度之和为 .
15. 若(2x﹣5)2+ =0,则2x+4y的平方根是 .16. 如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=3,CE=4,则两条凳子的高度之和为 . 17. 如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 .
17. 如图边长为1的正方形ABCD,AB在数轴上,点A在原点,点B对应的实数1,以A为圆心,AC长为半径逆时针画弧交数轴于点E,则点E对应的实数是 .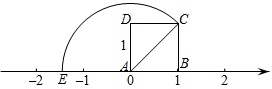
三、解答题
-
18. 计算:(1)、-(-)2+;(2)、|-3|-(+2)(-2).19. 如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD,若∠B=52°,∠C=43°.求∠DAC的度数.
 20. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.21. 如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.
20. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.21. 如图,△ABC的一个顶点A在△DEC的边DE上,AB交CD于点F,且AC=EC,∠1=∠2=∠3.试说明AB与DE的大小关系.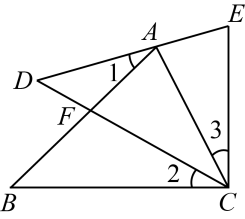 22. 如图,在直角坐标系内,已知点 .
22. 如图,在直角坐标系内,已知点 . (1)、图中点B的坐标是 ;(2)、点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;(3)、四边形ABCD的面积是 ;(4)、在y轴上找一点F,使 , 那么点F的坐标为 .23. 如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)、图中点B的坐标是 ;(2)、点B关于原点对称的点D的坐标是 ;点A关于y轴对称的点C的坐标是 ;(3)、四边形ABCD的面积是 ;(4)、在y轴上找一点F,使 , 那么点F的坐标为 .23. 如图,平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).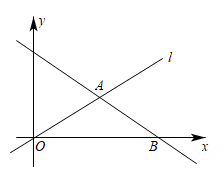 (1)、求直线l的表达式;(2)、求△AOB的面积;(3)、在直线l上求点P,使S△ABP=S△AOB.24. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
(1)、求直线l的表达式;(2)、求△AOB的面积;(3)、在直线l上求点P,使S△ABP=S△AOB.24. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且 ;按照方案二所需费用为 (元) ,且 其函数图象如图所示.
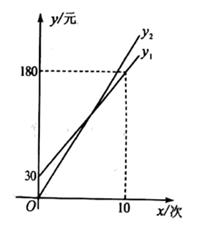 (1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
(1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.