山东省枣庄市薛城区2021-2022学年七年级上学期期末数学试题
试卷更新日期：2022-11-24 类型：期末考试
一、单选题
-
1. 汽车的雨刷把玻璃上的雨雪刷干净属于以下哪项几何知识的实际应用（ ）
A、点动成线 B、线动成面 C、面动成体 D、以上答案都符合题意2. 若x＝﹣1是关于x的方程2x+m＝1的解，则m+1的值是（ ）A、4 B、2 C、﹣2 D、﹣13. 在扇形统计图中，其中四个扇形的圆心角分别是30°，40°，50°，60°，则剩下的扇形是圆的（ ）A、 B、 C、 D、4.如图，四个有理数在数轴上的对应点M，P，N，Q，若点M，N表示的有理数互为相反数，则图中表示绝对值最小的数的点是（ ）
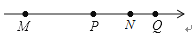A、点M B、点N C、点P D、点Q5. 如图，甲从A处出发沿北偏东60°向走向B处，乙从A处出发沿南偏西30°方向走到C处，则∠BAC的度数是 （ ）
A、 B、 C、 D、6. 如图，点C是AB的中点，AB＝10cm，CD＝2cm，则AD＝（ ）cm．
A、3 B、4 C、5 D、67. 如图，将甲，乙两把尺子拼在一起，两端重合，如果甲尺经校定是直的，那么乙尺不是直的，判断依据是（ ）
A、两点之间直线最短 B、经过一点有一条直线，并且只有一条直线 C、经过两点有一条直线，并且只有一条直线 D、线段可以向两个方向延长8. 如图，从8点钟开始，过了20分钟后，分针与时针所夹的度数是（ ）
A、 B、 C、 D、9. 《九章算术》记载了这样一道题：“以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺，问绳长井深各几何？”题意是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？假设井深为x尺，则正确的方程应为（ ）A、 B、3x+4＝4x+1 C、 D、3（x+4）＝4（x+1）10. 如图所示，已知数轴上点A表示的数为8，点B表示的数为-6．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动；动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，点P运动（ ）秒追上点Q．
A、5 B、6 C、7 D、811. 随着智能手机的普及，“支付宝支付”和“微信支付”等手机支付方式备受广大消费者的青睐，枣庄购物中心对2021年7-12月中使用这两种支付方式的情况进行统计，得到如图所示的折线图，根据统计图中的信息，得出以下四个推断，其中不合理的是（ ）
A、6个月中11月份使用手机支付的总次数最多 B、6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多 C、6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大 D、9月份平均每天使用手机支付的次数为0.314万次12. 我国海警舰艇编队于12月9日在我国钓鱼岛领海内进行巡航，巡航路线按照如下规律进行：从钓鱼岛O点出发，向东北方向航行1千米到达A点，从A点向西北方向航行1千米到达B点，从B点向西南方向航行1千米到达C点，从C点向东南方向航行1千米回到钓鱼岛O点，航行路线如图所示，那么航行2022千米后，我国海警的位置在（ ）点．
A、A B、B C、C D、O二、填空题
-
13. 对“神舟十三”的零部件检查的调查适合用调查．（填“全面”或“抽样”）14. 对于有理数a，b定义a⊙b＝2a－b，则（x＋y）⊙3x化简后得 ．15. 若∠α＝6.6°，∠β＝6°6′，则∠α∠β（填：“＞”，“＜”或“＝”）．16. 小明同学统计了某学校七年级部分同学每天阅读图书的时间，并绘制了统计图，如图所示．下面有四个推断：
①小明此次一共调查了100位同学；
②每天阅读图书时间不足15分钟的同学人数多于45-60分钟的人数；
③每天阅读图书时间在15-30分钟的人数最多；
④每天阅读图书时间超过30分钟的同学人数是调查总人数的20%．
根据图中信息，上述说法中正确的是 ． （直接填写序号）
17. 把一副三角尺按如图所示拼在一起，其中 ， ， 三点在同一直线上， 平分 ， 平分 ，则 .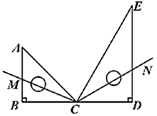
18. 枣庄购物中心将某种商品按原价的8折出售，此时商品的利润率是15%．已知这种商品的进价为2000元，那么这种商品的原价是元．三、解答题
-
19. 计算20. 解方程(1)、-3x-1＝2（2＋x）；(2)、 ．21. 为了防治“新型冠状病毒”，学校决定为师生购买一批医用口罩．已知甲种口罩每盒180元，乙种口罩每盒210元，学校购买了这两种口罩共50盒，合计花费9600元，求甲、乙两种口罩各购买了多少盒？22. 如图1，已知B、C在线段AD上．
(1)、图中共有条线段；(2)、若AB＝CD．①比较线段的大小：ACBD（填：“＞”、“＝”或“＜”）；
②如图2，若AD＝20，BC＝12，M是AB的中点，N是CD的中点，求MN的长度．
23. 网络学习已经被越来越多的学生所喜爱，某中学随机抽取了部分学生进行调查．要求每位学生从“优秀”，“良好”，“一般”，“不合格”四个等次中，选择一项作为自我评价网络学习的效果．现将调查的结果绘制成如图两幅不完整的统计图，请结合图中的所给信息解答下列问题．
(1)、这次活动共调查了名学生，扇形统计图中，等次为“良好”所占圆心角的度数是；(2)、请通过计算补全条形统计图；(3)、若该学校共有1200名学生，估计该学校网络学习等次为“优秀”的学生有多少人？24. 新定义：若∠的度数是∠的度数的n倍，则∠叫做∠的n倍角．
(1)、若∠M＝20°22′，请求出∠M的3倍角的度数；(2)、如图1，若∠AOB＝∠BOC＝∠COD，请直接写出图中∠AOB的所有2倍角；(3)、如图2，若∠AOC是∠AOB的3倍角，∠COD是∠AOB的4倍角，且∠BOD＝90°，求∠BOC的度数．25. 数轴是我们进入七年级后研究的一个很重要的数学工具，它让数变得形象，也让数轴上的点变得具体，借助数轴可以轻松的解决一些实际问题：已知数轴上的A、B两点分别对应的数字为a、b，且a，b满足|3b＋12|＋（a-3）2＝0．
(1)、a＝ ， b＝；(2)、P从B出发，以每秒2个长度的速度沿数轴负方向运动4秒，此时P点与A点之间的距离为；(3)、应用：小华家，小明家，学校在一条东西的大街上，小华家在学校的东面距学校500米，小明家在学校的西面距学校300米．
①画出如图的数轴（学校为原点，小华家为A点，小明家为B点），数轴的单位长度为实际的米．
②周末小明自西向东，小华自东向西出去玩，他们每分钟都走50米，求几分钟后两人相距100米？并直接写出此时小明在数轴上的位置对应的数．