山东省枣庄市台儿庄区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（）

A、总体是该校4000名学生的体重 B、个体是每一个学生 C、样本是抽取的400名学生的体重 D、样本容量是400

查看试题解析
2. 实数a、b、c在数轴上对应点的位置如图所示．如果 $a + b = 0$ ，那么下列结论正确的是（）

A、 $| a | > | c |$ B、 $a + c < 0$ C、 $a b c < 0$ D、 $\frac{a}{b} = 1$

查看试题解析
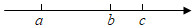3. 下列计算：① $2 a^{2} + 3 a^{2} = 5 a^{4}$ ；② $3 x^{3} y^{2} z - 2 x^{3} y^{3} z = 1$ ；③ $(- 2)^{5} - (- 5)^{2} = 0$ ；④ $| (- 7) \times (- 3) | = | - 7 | \times | - 3 |$ ．其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列去括号正确的是（）

A、 $x^{2} - (x - 3 y) = x^{2} - x - 3 y$ B、 $x^{2} - 3 (y^{2} - 2 x y) = x^{2} - 3 y^{2} + 2 x y$ C、 $a^{2} - 2 (a - 3) = a^{2} + 2 a - 6$ D、 $m^{2} - 4 (m - 1) = m^{2} - 4 m + 4$

查看试题解析
5. 方程 $2 - \frac{2 x - 4}{3} = - \frac{x - 7}{6}$ 去分母得（　　）

A、 $2 - 2 (2 x - 4) = - (x - 7)$ B、 $12 - 2 (2 x - 4) = - x - 7$ C、 $12 - (2 x - 4) = - (x - 7)$ D、 $12 - 2 (2 x - 4) = - (x - 7)$

查看试题解析
6. 线段AB=12cm，点C在线段AB上，且AC= $\frac{1}{3}$ BC，点M为BC的中点，则AM的长为（　　）

A、4.5cm B、6.5cm C、7.5cm D、8cm

查看试题解析
7. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）

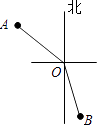A、69° B、111° C、141° D、159°

查看试题解析
8. 已知关于x的一元一次方程（3－a）x＋2a＝x＋2＋a的解是 $\frac{1}{3}$ 的倒数，则a的值为（　　）

A、－2 B、－1 C、1 D、2

查看试题解析
9. 如图是某天参观温州数学名人馆的学生人数统计图．若大学生有60人，则初中生有（）

A、45人 B、75人 C、120人 D、300人

查看试题解析
10. 某玩具商店周年店庆，全场八折促销，持会员卡可在促销活动的基础上再打六折．某电动汽车原价300元，小明持会员卡购买这个电动汽车需要花（）元

A、240 B、180 C、160 D、144

查看试题解析
11. 端午节买粽子，每个肉粽比素粽多1元，购买10个肉粽和5个素粽共用去70元，设每个肉粽x元，则可列方程为（）

A、 $10 x + 5 (x - 1) = 70$ B、 $10 x + 5 (x + 1) = 70$ C、 $10 (x - 1) + 5 x = 70$ D、 $10 (x + 1) + 5 x = 70$

查看试题解析
12. 对于任意的有理数 $a ， b$ ，如果满足 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ ，那么我们称这一对数 $a ， b$ 为“相随数对”，记为 $(a ， b)$ ．若 $(m ， n)$ 是“相随数对”，则 $3 m + 2 [3 m + (2 n - 1)] =$ （）

A、 $- 2$ B、 $- 1$ C、2 D、3

查看试题解析

二、填空题

13. 已知单项式 $2 a^{4} b^{- 2 m + 7}$ 与 $3 a^{2 m} b^{n + 2}$ 是同类项，则m+n= ．

查看试题解析
14. 如图是一个数值转换机的示意图，若输入x的值为3，y的值为 $- 2$ 时，则输出的结果为．

查看试题解析
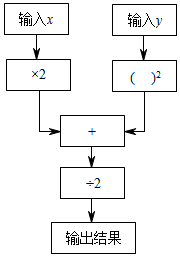15. 某种商品m千克的售价为n元，那么这种商品8千克的售价为元．

查看试题解析
16. 如图， $∠ A O B = 90 °$ ， $O D$ 平分 $∠ B O C$ ， $∠ A O C = 2 ∠ 1$ ，则 $∠ 1 =$ 度．

查看试题解析
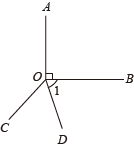17. 有一列数，按一定的规律排列成 $\frac{1}{3}$ ， $- 1$ ，3， $- 9$ ，27，－81，….若其中某三个相邻数的和是 $- 567$ ，则这三个数中第一个数是.

查看试题解析
18. 由一些大小相同的小正方体搭成的几何体，从正面看和从上面看的形状图如图所示，则搭成该几何体的小正方体的个数最少为个，搭成该几何体的小正方体的个数最多为个．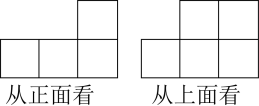

查看试题解析

三、解答题

19. 计算

(1)、 $- 2^{2} + (- 2) \times 3 - 1 \div (- 0.2) + | - 4 |$

(2)、 $- 7^{2} + 2 \times (- 3)^{2} - (- 6) \div (- \frac{1}{3})^{2}$

查看试题解析
20. 解方程

(1)、 $\frac{1}{5} x - 4 = 2 x + 3 - \frac{5}{2} x$

(2)、 $\frac{2 x - 4}{3} - (3 x + 2) = \frac{5}{2}$

查看试题解析
21. 某校为提高学生的综合素养，准备开展摄影、书法、绘画、表演、手工五类社团活动．为了对此项活动进行统筹安排，随机抽取了部分学生进行调查，要求每人从五个类别中只选择一个，将调查结果绘制成了两幅统计图（未完成）．请根据统计图中的信息，解答下列问题：

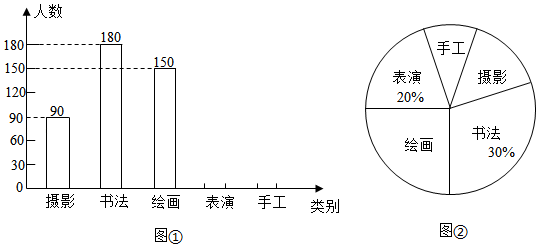(1)、本次共调查了名学生；

(2)、请将条形统计图补充完整；

(3)、扇形统计图中，“摄影”所占的百分比为；“手工”所对应的圆心角的度数为．

查看试题解析
22.
如图，已知A、B、C三点在同一直线上，AB=24cm，BC= $\frac{3}{8}$ AB，E是AC的中点，D是AB的中点，求DE的长．

查看试题解析
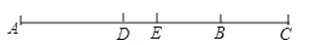23. 如图，由点O引出6条射线OA，OB，OC，OD，OE，OF，且∠AOB=90°，OF平分∠BOC，OE平分∠AOD，若∠EOF=170°，求∠COD的度数．

查看试题解析
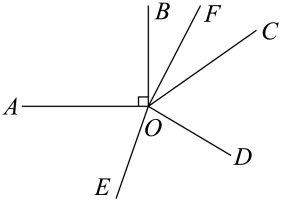24. 小丽放学回家后准备完成下面的题目：化简（□x²﹣6x+8）+（6x﹣5x²﹣2），发现系数“□“印刷不清楚．

(1)、她把“□”猜成3，请你化简（3x²﹣6x+8）+（6x﹣5x²﹣2）；

(2)、她妈妈说：你猜错了，我看到该题的标准答案是6．通过计算说明原题中“□”是几？

查看试题解析
25. 为了美化环境，建设生态桂林，某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积.

(1)、甲、乙两工程队每天各能完成多少平方米的绿化改造面积？

(2)、该社区需要进行绿化改造的区域共有12000平方米，甲队每天的施工费用为600元，乙队每天的施工费用为400元，比较以下三种方案：①甲队单独完成；②乙队单独完成；③甲、乙两队全程合作完成.哪一种方案的施工费用最少？

查看试题解析