山东省烟台市福山区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-24 类型:期末考试
一、单选题
-
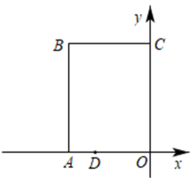
1. 在平面直角坐标系中,点 在第二象限内,则a的取值可以是( )A、1 B、 C、 D、4或-42. 下列图形中,是轴对称图形有( )

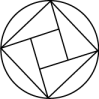
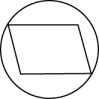 A、1个 B、2个 C、3个 D、4个3. 下列等式成立的是( )A、 B、 C、 D、4. 下列各数中,比3大比4小的无理数是( )A、3.14 B、 C、 D、5. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、
A、1个 B、2个 C、3个 D、4个3. 下列等式成立的是( )A、 B、 C、 D、4. 下列各数中,比3大比4小的无理数是( )A、3.14 B、 C、 D、5. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、 B、
B、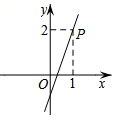 C、
C、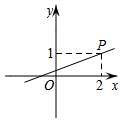 D、
D、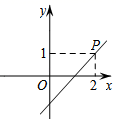 6. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
6. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )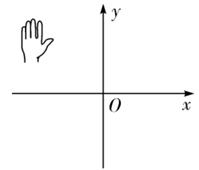 A、 B、 C、 D、7. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 为长的半径作弧,两弧在 内交于点F;作射线 交 于点G,若 ,P为 上一动点,则 的最小值为( )
A、 B、 C、 D、7. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 为长的半径作弧,两弧在 内交于点F;作射线 交 于点G,若 ,P为 上一动点,则 的最小值为( )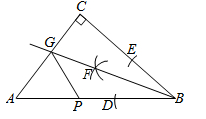 A、无法确定 B、 C、1 D、28. 如图,在平面直角坐标系中,的顶点都在格点上,如果将先沿y轴翻折,再向上平移3个单位长度,得到△ , 点B的对应点 , 那么关于x轴对称的点的坐标为( )
A、无法确定 B、 C、1 D、28. 如图,在平面直角坐标系中,的顶点都在格点上,如果将先沿y轴翻折,再向上平移3个单位长度,得到△ , 点B的对应点 , 那么关于x轴对称的点的坐标为( )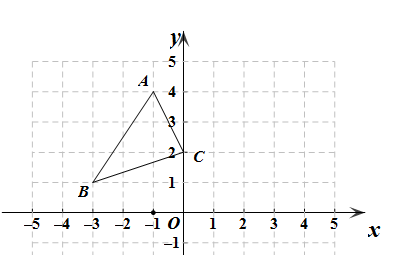 A、 B、 C、 D、9. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
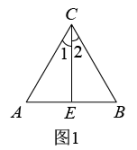
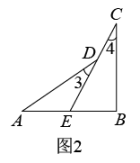
A、 B、 C、 D、9. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( ) A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,410. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( )
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,410. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( ) A、 寸 B、 寸 C、 寸 D、 寸11. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A、 寸 B、 寸 C、 寸 D、 寸11. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )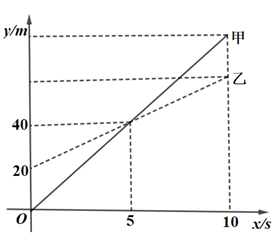 A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m12. 如图,棱柱的底面是边长为8的正方形,侧面都是长为16的长方形,点D是BC的中点,在棱柱下底面的A点处有一只蚂蚁,它想吃到上底面点D处的食物,需要爬行的最短路程是s,则s²的值为( )
A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m12. 如图,棱柱的底面是边长为8的正方形,侧面都是长为16的长方形,点D是BC的中点,在棱柱下底面的A点处有一只蚂蚁,它想吃到上底面点D处的食物,需要爬行的最短路程是s,则s²的值为( )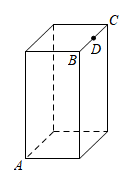 A、784 B、464 C、400 D、336
A、784 B、464 C、400 D、336二、填空题
-
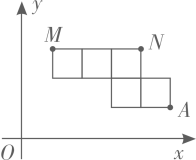
13. 若x是的算术平方根,y是-的立方根,则xy的值为 .14. 在平面直角坐标系中,点(4,-5)关于原点的对称点的坐标是 .15. 如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为.
 16. 如图,在矩形中, , 将向内翻折,点A 落在上,记为 , 折痕为 . 若将沿向内翻折,点B恰好落在上,记为 , 则 .
16. 如图,在矩形中, , 将向内翻折,点A 落在上,记为 , 折痕为 . 若将沿向内翻折,点B恰好落在上,记为 , 则 .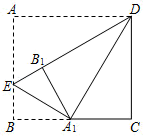 17. 如图,AB=18m,CA⊥AB于A,DB⊥AB于B,且AC=6m,点P从B向A运动,每秒钟走1m,Q点从B向D运动,每秒钟走2m,点P,Q同时出发,运动秒后,△CAP与△PQB全等.
17. 如图,AB=18m,CA⊥AB于A,DB⊥AB于B,且AC=6m,点P从B向A运动,每秒钟走1m,Q点从B向D运动,每秒钟走2m,点P,Q同时出发,运动秒后,△CAP与△PQB全等.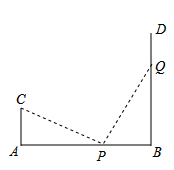 18. 如图,动点P从坐标原点出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点 , 第2秒运动到点 , 第3秒运动到点 , 第4秒运动到点则第120秒时点P所在位置的坐标是 .
18. 如图,动点P从坐标原点出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点 , 第2秒运动到点 , 第3秒运动到点 , 第4秒运动到点则第120秒时点P所在位置的坐标是 .
三、解答题
-
19. 计算:(1)、(2)、20. 已知:实数a,b满足关系式 , 请求出的值.21. 如图是某校的平面示意图,其中A-校门,K-旗杆,B,C-教学楼,E-实验楼,D-运动场,F-餐厅,H-图书馆,G-宿舍区,(每格代表1cm)回答如下问题:
 (1)、图书馆位于校门口的方向上,距离校门约米.(2)、在校门口的东北方向上,有以下建筑物: .(3)、如果用表示校门的位置,那么宿舍区的位置是 , 旗杆的位置是 , 点表示的是 .22. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: .
(1)、图书馆位于校门口的方向上,距离校门约米.(2)、在校门口的东北方向上,有以下建筑物: .(3)、如果用表示校门的位置,那么宿舍区的位置是 , 旗杆的位置是 , 点表示的是 .22. 如图,在四边形 中, ,点E,F分别在 , 上, , ,求证: . 23. 我国传统的计重工具--秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
23. 我国传统的计重工具--秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.x(厘米)
1
2
4
7
11
12
y(斤)
0.75
1.00
1.50
2.75
3.25
3.50
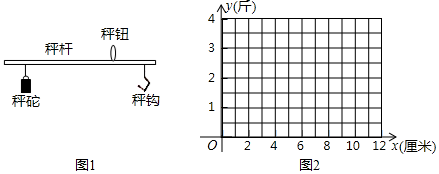 (1)、在上表x,y的数据中,发现有一对数据记录不符合题意.在图2中,通过描点的方法,观察判断哪一对是错误的?(2)、根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?24. 某鲜花销售公司每月付给销售人员的工资有两种方案.
(1)、在上表x,y的数据中,发现有一对数据记录不符合题意.在图2中,通过描点的方法,观察判断哪一对是错误的?(2)、根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?24. 某鲜花销售公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
如图中的射线 , 射线分别表示该鲜花销售公司每月按方案一,方案二付给销售人员的工资(单位:元)和(单位:元)与其当月鲜花销售量x(单位:千克)()的函数关系.
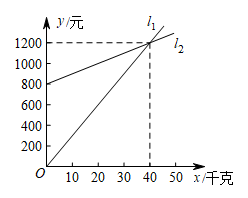 (1)、分别求﹑与x的函数解析式(解析式也称表达式);(2)、若该公司某销售人员12月份的鲜花销售量没有超过60千克,但其12月份的工资超过1500元.这个公司采用了哪种方案给这名销售人员付12月份的工资?
(1)、分别求﹑与x的函数解析式(解析式也称表达式);(2)、若该公司某销售人员12月份的鲜花销售量没有超过60千克,但其12月份的工资超过1500元.这个公司采用了哪种方案给这名销售人员付12月份的工资?