山东省威海市乳山市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 5的算术平方根是（）

A、25 B、± $\sqrt{5}$ C、 $\sqrt{5}$ D、﹣ $\sqrt{5}$

查看试题解析
2. 下面是同学们设计的一些美丽有趣的图案，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，ΔABC≌ΔDCB，若AC＝7，BE﹦5，则DE的长为（）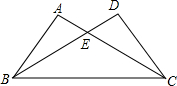

A、2 B、3 C、4 D、5

查看试题解析
4.
如图，一架长为10m的梯子斜靠在一面墙上，梯子底端离墙6m，如果梯子的顶端下滑了2m，那么梯子底部在水平方向滑动了（　　）

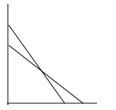A、2m B、2.5m C、3m D、3.5m

查看试题解析
5. 直线l₁：y＝2x+1与直线l₂关于y轴对称，直线l₂的表达式为（）

A、y＝﹣2x+1 B、y＝2x﹣1 C、y＝﹣2x﹣1 D、y＝x+2

查看试题解析
6. 在平面直角坐标系中，A（-1，0），B（5，0），C（2，5），则△ABC的面积为（）

A、15 B、20 C、30 D、10

查看试题解析
7. 如图，已知 $A B = A C$ ， $A E = A D$ ，则图中全等的三角形共有（）

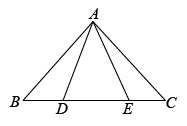A、2对 B、3对 C、4对 D、5对

查看试题解析
8. 如图，大正方形是由49个边长为l的小正方形拼成的，A，B，C，D四个点是小正方形的顶点，由其中三个点为顶点的直角三角形的个数是（）

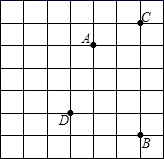A、1 B、2 C、3 D、4

查看试题解析
9. 如图，点A是第二象限内一点，OA=2，且OA与x轴正半轴的夹角为 $120 °$ ，则点A的坐标为（）

A、 $(\sqrt{3} ， 1)$ B、 $(- \sqrt{3} ， 1)$ C、 $(1 ， \sqrt{3})$ D、 $(- 1 ， \sqrt{3})$

查看试题解析
10. 如图，在△ABC中，AB=10，BC=7，AC=6，沿过点B的直线折叠△ABC，使点C落在AB边上的点E处，折痕为BD，则△AED的周长为（）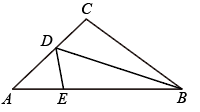

A、6 B、7 C、9 D、10

查看试题解析

二、多选题

11. 通过估算比较大小，下列结论正确的是（）

A、 $\sqrt[3]{69} > \sqrt{16}$ B、 $- \sqrt{10} > \sqrt[3]{- 27}$ C、 $\frac{\sqrt{7} - 2}{2} < \frac{1}{2}$ D、 $\sqrt{15} < 2 \sqrt{5}$

查看试题解析
12. 如图，在△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC．下列结论正确的是（）

A、∠BAD=∠C B、AE=AF C、∠EBC=∠C D、GF=GE

查看试题解析

三、填空题

13. $\sqrt[3]{- \frac{1}{64}}$ = ．

查看试题解析
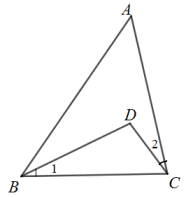
14. 若点P（m+3，m+1）在x轴上，则点P的坐标为．

查看试题解析
15. 如图，D是△ABC内一点，∠ACB=70°，∠1=∠2，则∠D=°．

查看试题解析
16. 函数y＝2x﹣4的图象与两条坐标轴所围成的三角形的面积是．

查看试题解析
17. 如图，由四个全等的直角三角形和一个小正方形拼成一个大正方形．已知直角三角形的短直角边长为3，小正方形的面积为1，则大正方形的面积为．

查看试题解析
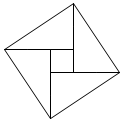18. 已知 $\sqrt{17}$ －2的整数部分为a， $\sqrt{17}$ +2的整数部分为b，那么b－a的平方根是．

查看试题解析

四、解答题

19. 计算： $\sqrt{{(- 3)}^{2}} - 2 \times \sqrt{\frac{9}{4}} + \frac{5}{2} \times \sqrt[3]{- 0.027}$ ．

查看试题解析
20. 如图，四边形ABCD中，∠ADC=90°，AD=4cm，CD=3cm，AB=13cm，BC=12cm，求这个四边形的面积？

查看试题解析
21. 【材料阅读】
在平面直角坐标系中，过一点分别作两坐标轴的垂线，若两条垂线段与坐标轴围成的长方形周长的数值与面积的数值相等，则这个点叫做“和谐点”．
如图，过点P分别作x，y轴的垂线，与坐标轴围成的长方形OAPB周长的数值与面积的数值相等，则点P是“和谐点”．

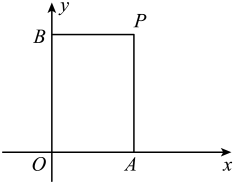(1)、点M（1，2）是 “和谐点”吗？为什么？

(2)、若“和谐点”P（a，3）（a＞0）在直线y=-x+b（b为常数）上，求a，b的值．

查看试题解析
22. 如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF∥AB交DE的延长线于点F．

(1)、证明：△ADE≌△CFE；

(2)、若∠B＝∠ACB，CE＝5，CF＝7，求DB．

查看试题解析
23. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与x，y轴交于点A，B（0，4），与正比例函数y=-2x的图象相交于点C（-1，m）

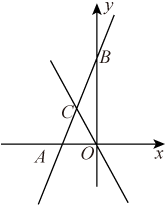(1)、求一次函数 $y = k x + b$ 的表达式；

(2)、若点P在直线AB上，且 $S_{△ O A P} = 3 S_{△ O A C}$ ，求点P的坐标．

查看试题解析
24. 如图，△ABC中，∠A=60°．

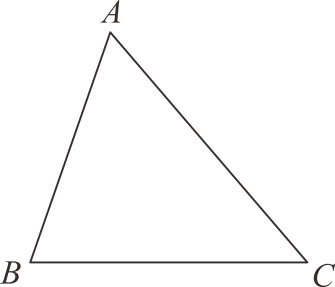(1)、求作一点P，使得点P到B、C两点的距离相等，并且点P到AB、BC的距离也相等（尺规作图，不写作法，保留作图痕迹）；

(2)、在（1）的条件下，若∠ACP=15°，求∠ABP的度数．

查看试题解析
25. 如图，AE与BD交于点C，AC=EC，BC=DC，AB=6cm，点P从A出发，沿A→B→A的方向以3cm/s的速度运动；点Q从D出发，沿D→E的方向以1cm/s的速度运动．点P，Q同时出发，当点P到达A时，P，Q两点同时停止运动．设点P的运动时间为t（s）．

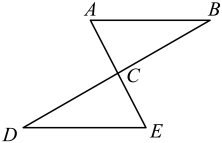(1)、直接写出线段BP的长；（用含t的式子表示）

(2)、连接PQ，当线段PQ经过点C时，求t的值．

查看试题解析