山东省泰安市泰山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数： $\sqrt{7} ， - 0.6 ， \sqrt[3]{5} ， π ， - \frac{3}{11} ， 0.131331333133331 ⋯$ （每两个1之间依次增加一个3），其中无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列四个图形中，是轴对称图形的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 在 $△ A B C$ 与 $△ D F E$ 中， $∠ B = ∠ F ， A B = D F$ ，添加下列条件后，仍不能得到 $△ A B C ≌ △ D F E$ 的是（）

A、 $B C = E F$ B、 $B E = C F$ C、 $A C = D E$ D、 $∠ A = ∠ D$

查看试题解析
4. 实数 $- 1 ， 0 ， - \sqrt{3} ， - \sqrt{2}$ 中，最小的数是（）

A、 $- 1$ B、 $- \sqrt{2}$ C、0 D、 $- \sqrt{3}$

查看试题解析
5. 如图， $A E / / B D$ ， $∠ 1 = 11 5^{∘}$ ， $∠ 2 = 3 5^{∘}$ ，则∠C的度数是（）

A、 $3 0^{∘}$ B、 $3 5^{∘}$ C、 $4 0^{∘}$ D、 $5 0^{∘}$

查看试题解析
6. 下列描述一次函数 $y = - 2 x + 5$ 的图象及性质错误的是（）

A、直线与x轴交点坐标是 $(0 ， 5)$ B、y随x的增大而减小 C、直线经过第一、二、四象限 D、当 $x < 0$ 时， $y > 5$

查看试题解析
7. 若长度分别是a、6、10的三条线段能组成一个三角形，则a的值可以是（）

A、16 B、8 C、4 D、2

查看试题解析
8. 如果 $\sqrt{a^{2}} = - a$ ，则一次函数 $y = (a - 1) x + 2 - a$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 以下判断中错误的是（）

A、等边三角形的每条高线都是角平分线和中线 B、有一内角为 $60 °$ 的等腰三角形是等边三角形 C、等腰三角形一定是锐角三角形 D、等腰三角形顶角的平分线，底边上的中线，底边上的高相互重合

查看试题解析
10. 下列说法：① $- 2$ 是4的平方根；② $a^{2}$ 的算术平方根是a；③ $1 0^{- 2}$ 的算术平方根是 $\frac{1}{10}$ ；④平方根和立方根都等于本身的数是0和1；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，保持△ABC的三个顶点的横坐标不变，纵坐标都乘-1，画出坐标变化后的三角形，则所得三角形与原三角形的关系是（　　）

A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位

查看试题解析
12. 如图， $A B$ 、 $B C$ 、 $C D$ 、 $D E$ 是四根长度均为5cm的火柴棒，点A、C、E共线.若 $A C = 6 cm$ ， $C D ⊥ B C$ ，则线段 $C E$ 的长度为（）

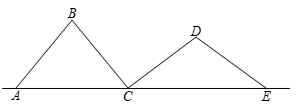A、6 cm B、7 cm C、 $6 \sqrt{2} cm$ D、8cm

查看试题解析

二、填空题

13. 点 $P (- 2 ， - 5)$ 在平面直角坐标系中关于y轴的对称点坐标是．

查看试题解析
14. 在一次函数 $y = - x + 3$ 中，当 $x > 1$ 时，y ．

查看试题解析
15. $\sqrt{9}$ 的平方根是

查看试题解析
16. 如图所示，在等边三角形 $A B C$ 中， $A D ⊥ B C$ ， E为 $A D$ 上一点， $∠ C E D = 65 °$ ，则 $∠ A B E$ 的度数是．

查看试题解析
17. 已知一个正数的两个平方根分别是 $x + 5$ 与 $3 x - 17$ ，那么这个正数是．

查看试题解析
18. 如图所示，延长△ABC的中线AD到点E，使 $D E = A D$ ，连接BE，EC，那么在四边形ABEC中共有对全等的三角形．

查看试题解析
19. 如图， $△ O A_{1} A_{2}$ 是等腰直角三角形， $O A_{1} = 1$ ，以斜边 $O A_{2}$ 为直角边作等腰直角三角形 $O A_{2} A_{3}$ ，再以 $O A_{3}$ 为直角边作等腰直角三角形 $O A_{3} A_{4}$ …，按此规律作下去，则 $O A_{2021}$ 的长为．

查看试题解析
20. 如图，已知一次函数 $y = k x + b$ 的图象与x轴，y轴分别交于点 $(2 ， 0)$ ，点 $(0 ， 3)$ ，有下列结论：①图象经过点 $(1 ， - 3)$ ；②关于x的方程 $k x + b = 0$ 的解为 $x = 2$ ；③关于x的方程 $k x + b = 3$ 的解为 $x = 0$ ；④当 $x > 2$ 时， $y < 0$ ．其是正确的是．

查看试题解析

三、解答题

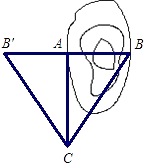
21. 已知如图，要测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，对吗？为什么？

查看试题解析
22. 计算

(1)、 $\sqrt{36} + \sqrt[3]{- 27} - \sqrt{(- 4)^{2}} + | \sqrt{5} - 3 |$ ；

(2)、已知x是25的算术平方根，y是64的平方根，求 $2 x^{2} - y^{2} + 4 x + 3$ 的值．

查看试题解析
23. 如图所示，一个梯子 $A B$ 长2.5米，顶端A靠在墙 $A B$ 上，这时梯子下端B与墙角C距离为0.7米．如果梯子的顶端A下滑0.4米到了点E的位置，那么梯子的底端B在水平方向滑动了0.4米吗？为什么？

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B = 30 °$ ，线段 $A B$ 的垂直平分线 $M N$ 交 $B C$ 于 $D$ ，求证： $C D = 2 B D$ .

查看试题解析
25. 计算： $△ A B C$ 在平面直角坐标系 $x O y$ 中的位置如图所示．
( 1 )作 $△ A B C$ 关于y轴成轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1} 、 B_{1} 、 C_{1}$ 的坐标；
( 2 )在y轴上有一点P，使 $P A + P B$ 的值最小，请在坐标系中标出点P的位置．

查看试题解析
26. 如图，已知函数 $y_{1} = x + 2$ 的图象与y轴交于点A，一次函数 $y_{2} = k x + b$ 的图象经过点 $B (0 ， 4)$ ，与x轴交于点C，与 $y_{1} = x + 2$ 的图象交于点D，且点D的坐标为 $(\frac{1}{2} ， n)$

(1)、求k和b的值；

(2)、若 $y_{1} > y_{2}$ ，写出x的取值范围；

(3)、求四边形 $A O C D$ 的面积．

查看试题解析
27. 剧院举行新年专场音乐会，成人票每张80元，学生票每张40元，剧院制定了两种优惠方案，方案1：购买一张成人票赠送一张学生票；方案2：按总价的 $80 %$ 付款．某校有5名老师与若干名（不少于5人）学生听音乐会

(1)、设学生人数为x（人），付款总金额为y（元），分别表示这两种方案；

(2)、当学生人数为多少人时，两种方案的费用相同？

(3)、若现有30名学生，则哪种方案费用更少？

查看试题解析