山东省泰安市宁阳县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数：-2，0， $\frac{1}{3}$ ，0.020020002…， $π$ ， $\sqrt{9}$ ，其中无理数的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt[3]{- 5} = \sqrt[3]{5}$ C、 $\sqrt{36} = \pm 6$ D、 $- \sqrt{0.36} =-0 .6$

查看试题解析
3. 在学习《图形变化的简单应用》这一节时，老师要求同学们利用图形变化设计图案．下列设计的图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，AB∥CD，∠D＝42°，∠CBA＝64°，则∠CBD的度数是（）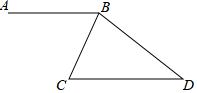

A、42° B、64° C、74° D、106°

查看试题解析
5. 若y²+4y+4+ $\sqrt{x + y - 1}$ ＝0，则xy的值为（）

A、﹣6 B、﹣2 C、2 D、6

查看试题解析
6. 下列图象中，不能表示y是x的函数的是（）

A、 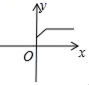B、 C、 D、

查看试题解析
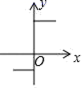7. 点 $A (a - 1 ， 5)$ 和点 $B (2 ， b - 1)$ 关于x轴对称，则 ${(a + b)}^{2021} =$ （）

A、1 B、 $- 1$ C、 $\pm 1$ D、0

查看试题解析
8. 直线y=ax+b经过第一、二、四象限，则直线y=bx+a的图象只能是图中的（）

A、 B、 C、 D、

查看试题解析
9. 如图，已知在 $△ A O B$ 中 $A (0 ， 4) ， B (- 2 ， 0)$ ，点M从点 $(4 ， 1)$ 出发向左平移，当点M平移到 $A B$ 边上时，平移距离为（）

A、 $4.5$ B、 $5$ C、 $5.5$ D、 $5.75$

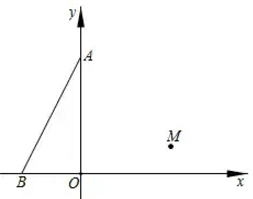查看试题解析
10. 如图，在四边形ABCD中， $A D ∥ B C$ ， $∠ D = 90 °$ ， $A D = 5$ ， $B C = 3$ ．分别以点A，C为圆心，大于 $\frac{1}{2} A C$ 长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（）

A、 $\sqrt{5}$ B、4 C、3 D、 $\sqrt{10}$

查看试题解析
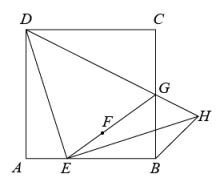
11. 如图是由8个全等的长方形组成的大正方形，线段AB的端点都在小长方形的顶点上，如果点P是某个小长方形的顶点，连接PA，PB，那么使△ABP为等腰三角形的点P的个数是（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
12. 如图，在 $△ O A B$ 和 $△ O C D$ 中， $O A = O B ， O C = O D ， O A > O C ， ∠ A O B = ∠ C O D = 40 °$ ，连接 $A C ， B D$ 交于点 $M$ ，连接 $O M$ ．下列结论：① $A C = B D$ ；② $∠ A M B = 40 °$ ；③ $O M$ 平分 $∠ B O C$ ；④ $M O$ 平分 $∠ B M C$ ．其中正确的个数为（）．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

13. 若等腰三角形两边x、y满足 $y = \sqrt{x - 2} + \sqrt{2 - x} + 4$ ，等腰三角形的周长为．

查看试题解析
14. 一次函数 $y = a x + b$ 与两坐标轴的交点为 $(- 2 ， 0)$ 、 $(0 ， 3)$ ，则关于x的方程的 $a x + b = 0$ 解是．

查看试题解析
15. 如图，一艘轮船以每小时20海里的速度沿正北方航行，在A处测得灯塔C在北偏西30°方向上，轮船航行2小时后到达B处，在B处测得灯塔C在北偏西60°方向上，当轮船到达灯塔C的正东方B向D处时，则轮船航程AD的距离是海里．

查看试题解析
16. 如图，已知边长为2的正方形OABC在平面直角坐标系中，点A位于第一象限内B、C两点在第二象限内，OA与x轴所夹锐角为60°．则C点的坐标为．

查看试题解析
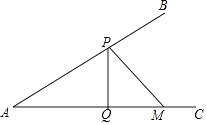
17.
如图，∠BAC=30°，M为AC上一点，AM=2，点P是AB上的一动点，PQ⊥AC，垂足为点Q，则PM+PQ的最小值为．

查看试题解析
18. 如图，在平面直角坐标系中，将 $Δ A B O$ 绕点A顺时针旋转到△ $A B_{1} C_{1}$ 的位置，点B、O分别落在点 $B_{1}$ 、 $C_{1}$ 处，点 $B_{1}$ 在x轴上，再将△ $A B_{1} C_{1}$ 绕点 $B_{1}$ 顺时针旋转到△ $A_{1} B_{1} C_{2}$ 的位置，点 $C_{2}$ 在x轴上，将△ $A_{1} B_{1} C_{2}$ 绕点 $C_{2}$ 顺时针旋转到△ $A_{2} B_{2} C_{2}$ 的位置，点 $A_{2}$ 在x轴上，依次进行下去 $\dots$ ，若点 $A (\frac{5}{3}$ ， $0)$ 、 $B (0 ， 4)$ ，则点 $B_{2022}$ 的横坐标为．

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{25} + \sqrt[3]{- \frac{1}{8}} - \sqrt{{(- 3)}^{2}} - \sqrt{1 \frac{7}{9}}$

(2)、 $\sqrt{16} + \sqrt[3]{- 27} + 3 \sqrt{3} - \sqrt{{(- 4)}^{2}}$

(3)、 $\sqrt{64} - \sqrt[3]{\frac{1}{8}} + {(- \frac{2}{3})}^{- 2} + {(π - 3.14)}^{0} - {(\sqrt{\frac{3}{2}})}^{2}$

(4)、 $\sqrt[3]{- 8} - \sqrt{1 - \frac{16}{25}} + | 2 - \sqrt{5} | + \sqrt{{(- 4)}^{2}} - 1^{2022}$

(5)、 $6 \times \sqrt{\frac{1}{9}} - \sqrt[3]{27} + {(\sqrt{2})}^{2} - \sqrt{4^{2} - 3^{2}}$

查看试题解析
20. 解答

(1)、求下列x的值：
① $2 x^{2} = 72$ ；
② ${(x + 1)}^{3} + 3 = - 61$ ．

(2)、已知一个正数的两个平方根分别是 $a + 3$ 和 $2 a - 15$ ．
①求这个正数；
②求 $\sqrt{a + 12}$ 的平方根．

查看试题解析
21. 公司销售部门提供了某种产品销售收入(记为： $y_{1}$ /元)、销售成本(记为： $y_{2}$ /元)、销售量(记为： x/吨)方面的信息如下：
① $x = 0$ 时， $y_{2} = 2000$ ；
② $x = 2$ 时， $y_{1} = 2000 ，$ $y_{2} = 3000$ ；
③ $y_{1}$ 与x成正比例函数关系；④ $y_{2}$ 与x成一次函数关系．
依据上述信息，解决下列问题：

(1)、分别求出 $y_{1} ， y_{2}$ 与x的函数关系式；

(2)、销售量为多少吨时，销售收入与销售成本相同?

(3)、若销售量为6吨时，求公司的利润． (利润=销售收入-销售成本)

查看试题解析
22. 如图，AD是△ABC的中线，点E在AD上，且BE＝AC，求证：∠BED＝∠CAD．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $l_{1} ： y = \frac{1}{2} x$ 与直线 $l_{2} ： y = - \frac{3}{2} x + b$ 交点A的横坐标为2，将直线 $l_{1}$ ，沿y轴向下平移4个单位长度，得到直线 $l_{3}$ ，直线 $l_{3}$ 与y轴交于点B，与直线 $l_{2}$ 交于点C，直线 $l_{2}$ 与y轴交于点D．

(1)、求直线 $l_{2}$ 、 $l_{3}$ 的表达式；

(2)、求C点坐标；

(3)、求△BDC的面积．

查看试题解析
24. 如图1，△ABC和△DEC均为等腰直角三角形，∠ACB=∠DCE=90°，点B，D，E在同一直线上，连接AD，BD．

(1)、请探究AD与BD之间的位置关系并证明你的结论；

(2)、若AC=BC= $\sqrt{10}$ ， DC=CE= $\sqrt{2}$ ，求线段AD的长；

查看试题解析
25. 如图，在正方形ABCD中，E是边AB上的一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，且∠CGD＝∠DGE，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．

(1)、猜想：△DEH的形状，并说明理由．

(2)、猜想BH与AE的数量关系，并证明．

查看试题解析