山东省青岛市崂山区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-24 类型:期末考试
一、单选题
-
1. 的倒数是( )A、-2 B、 C、 D、22. 天王星围绕太阳公转的轨道半径为2900000000千米.将数字2900000000千米用科学记数法表示为( )千米。A、0.29×1010 B、2.9×1010 C、2.9×109 D、29×1083. 下列说法正确的是( )A、连接两点的线段叫做这两点的距离 B、两点之间,直线最短 C、若 , 则点P为线段为的中点 D、过两点有且只有一条直线4. 下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是( )
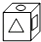 A、
A、 B、
B、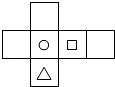 C、
C、 D、
D、 5. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量6. 若m2+2m=3,则4m2+8m﹣1的值是( )A、11 B、8 C、7 D、127. 关于的方程的解是 , 则的值为( ).A、4 B、-4 C、5 D、-58. 如图,将 , , , 0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a,b,c分别表示其中的一个数,则的值为( )
5. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量6. 若m2+2m=3,则4m2+8m﹣1的值是( )A、11 B、8 C、7 D、127. 关于的方程的解是 , 则的值为( ).A、4 B、-4 C、5 D、-58. 如图,将 , , , 0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a,b,c分别表示其中的一个数,则的值为( )4
a
2
1
3
b
5
c
A、5 B、 C、0 D、二、填空题
-
9. 与 是同类项,则 mn = .10. 冰箱开始启动时的内部温度为8℃,若每小时冰箱内部的温度降低5℃,那么3小时后冰箱内部的温度是℃.11. 如图,点C是线段AB上一点,且 , , 若点O为线段AB的中点,则线段OC的长为cm;
 12. 一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为 .13. 观察下列等式:13=12 , 13+23=32 , 13+23+33=62 , 13+23+33+43=102…根据等式左边各项幂的底数与等式右边幂的底数的关系,写出第n个等式14. 一个由13个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,则这个几何体的搭法共有种.
12. 一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为 .13. 观察下列等式:13=12 , 13+23=32 , 13+23+33=62 , 13+23+33+43=102…根据等式左边各项幂的底数与等式右边幂的底数的关系,写出第n个等式14. 一个由13个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,则这个几何体的搭法共有种.
三、解答题
-
15. 尺规作图.
如图,已知在平面上有三个点A,B,C,请按下列要求作图:

⑴作直线AB;
⑵作射线AC;
⑶在射线AC上作线段AD,使AD=2AB.
16. 计算:(1)、;(2)、;(3)、先化简,后求值: , 其中k=;(4)、解方程: .17. 某校对七年级300名学生进行了教学质量检测(满分100分),现从中随机抽取部分学生的成绩进行整理,并绘制成如图不完整的统计表和统计图:等级
频数
频率(频率=频数÷总数)
不及格
1
0.05
及格
2
0.10
良好
a
0.45
优秀
8
b
注:60分以下为“不及格”,60~69分为“及格”,70~79为“良好”,80分及以上为“优秀”

请根据以上信息回答下列问题:
(1)、求出a,b值,并补全统计图;(2)、若用扇形统计图表示统计结果,则“良好”所对应扇形的圆心角为多少度?(3)、请估计该校七年级本次监测成绩为70分及以上的学生共有多少人?18. 某水泥仓库一周7天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):+30,-26,-30,+27,-29,-16,-15.(1)、经过这7天,仓库里的水泥是增多还是减少了?增多或减少了多少吨?(2)、经过这7天,仓库管理员结算发现库里还存100吨水泥,那么7天前,仓库里存有水泥多少吨?(3)、如果进仓库的水泥装卸费是每吨m元、出仓库的水泥装卸费是每吨n元,求这7天要付多少元装卸费?19. 如图,O是直线AB上一点,∠AOE=∠COD,射线OC平分∠BOE,∠EOC=50°.求∠DOE的度数. 20. “双十二”期间,某商场将一款羽绒服成本价提高后标价,接着又以8折优惠卖出,结果每件羽绒服仍可获利21元,那么这款羽线服的成本价是多少元?21. 如图①是一张长为20cm,宽为12cm的长方形硬纸板,把它的四个角都剪去一个边长为x cm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
20. “双十二”期间,某商场将一款羽绒服成本价提高后标价,接着又以8折优惠卖出,结果每件羽绒服仍可获利21元,那么这款羽线服的成本价是多少元?21. 如图①是一张长为20cm,宽为12cm的长方形硬纸板,把它的四个角都剪去一个边长为x cm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题: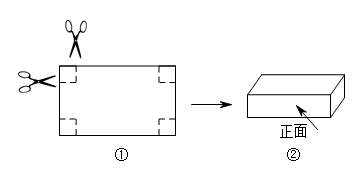 (1)、折成的无盖长方体盒子的容积;(用含x的代数式表示即可,不需化简)(2)、请写出a,b值;
(1)、折成的无盖长方体盒子的容积;(用含x的代数式表示即可,不需化简)(2)、请写出a,b值;1
2
3
4
5
180
a
252
192
b
(3)、从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出的值;如果不是正方形,请说明理由.22. 经过A,B两地有一条直路,小明和小亮约好上午8点分别从A,B两地同时出发相向而行,分别做匀速运动,则上午10点两人相距18km,中午12点两人又相距18km.已知小明每小时比小亮多走2km.请根据以上信息解答下列问题:(1)、小明和小亮的速度各是多少?(2)、A,B两地的距离是多少?23. 我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非.”数形结合的思想方法在数学中应用极为广泛.观察下列按照一定规律堆砌的钢管的横截面图:

用含n的式子表示第n个图的钢管总数.
【分析思路】
图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律.
如:要解决上面问题,我们不妨先从特例入手: (统一用S表示钢管总数)
【解决问题】
(1)、如图,如果把每个图形按照它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.
S=1+2 S=2+3+4
(2)、其实,对同一个图形,我们的分析眼光可以是不同的.请你像(1)那样保持结构的、对每一个所给图形添加分割线,提供与(1)不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律: (3)、用含n的式子列式,并计算第n个图的钢管总数.24. 如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(3)、用含n的式子列式,并计算第n个图的钢管总数.24. 如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒. (1)、当t=2时,点P对应的有理数xP= , PQ=;(2)、当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;(3)、我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.
(1)、当t=2时,点P对应的有理数xP= , PQ=;(2)、当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;(3)、我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.