2022-2023学年冀教版数学八上期末复习专题9 直角三角形全等的判定和反证法
试卷更新日期:2022-11-24 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 如图,在△ABC中, , D是上一点,于点E, , 连接 , 若 , 则等于( )
 A、6 B、7 C、8 D、92. 如图, , 且 , 则判定≌的最好理由是( )
A、6 B、7 C、8 D、92. 如图, , 且 , 则判定≌的最好理由是( ) A、 B、 C、 D、3. 如图所示,在△ABC中,AB=AC,∠B=∠C,D、E在BC上,BD=CE,AF⊥BC于F,则图中全等三角形的对数为( )
A、 B、 C、 D、3. 如图所示,在△ABC中,AB=AC,∠B=∠C,D、E在BC上,BD=CE,AF⊥BC于F,则图中全等三角形的对数为( ) A、1 B、2 C、3 D、44. 要说明命题“若a2>b2 , 则a>b”是假命题,能举的一个反例是( )A、a=3,b=2 B、a﹣3,b=2 C、a﹣=3,b=﹣1 D、a=﹣1,b=35. 如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( )
A、1 B、2 C、3 D、44. 要说明命题“若a2>b2 , 则a>b”是假命题,能举的一个反例是( )A、a=3,b=2 B、a﹣3,b=2 C、a﹣=3,b=﹣1 D、a=﹣1,b=35. 如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( ) A、BD=AD B、∠B=∠C C、AD=CD D、∠BAD=∠ACD6. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( )
A、BD=AD B、∠B=∠C C、AD=CD D、∠BAD=∠ACD6. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( ) A、8cm B、10cm C、12cm D、14cm7. 如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( )
A、8cm B、10cm C、12cm D、14cm7. 如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( ) A、SAS B、AAS C、SSS D、HL8. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( )
A、SAS B、AAS C、SSS D、HL8. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③9. 用反证法证明:在 中, 中不能有两个角是钝角时,假设 中有两个角是钝角,令 ,则所得结论与下列四个选项相矛盾的是( )A、已知 B、三角形内角和等于 C、钝角三角形的定义 D、以上结论都不对10. 如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( )
A、①②④ B、①②③④ C、②③④ D、①③9. 用反证法证明:在 中, 中不能有两个角是钝角时,假设 中有两个角是钝角,令 ,则所得结论与下列四个选项相矛盾的是( )A、已知 B、三角形内角和等于 C、钝角三角形的定义 D、以上结论都不对10. 如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题(每题3分,共18分)
-
11. 已知△ABC中,AB=AC,求证:∠B<90°,用反证法证明:第一步是:假设12. 如图,中, , 点D在上,且于点E , , 若 , 则.
 13. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可)
13. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可) 14. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF= .
14. 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF= . 15. 如图, , , 于点 , 于点 , , ,则 的长是 .
15. 如图, , , 于点 , 于点 , , ,则 的长是 .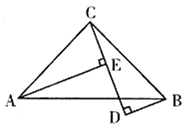 16. 在 中, , , , 于 , , 两点分别在边 和射线 上移动.当 , 时, 和 全等.
16. 在 中, , , , 于 , , 两点分别在边 和射线 上移动.当 , 时, 和 全等.
三、解答题(共5题,共52分)
-
17. 如图, , E是上的一点,且 , .
求证:≌
 18. 如图,、相交于点 , , 于点 , 于点 , 且 .
18. 如图,、相交于点 , , 于点 , 于点 , 且 .求证: .
 19. 阅读下列文字,回答问题.
19. 阅读下列文字,回答问题.题目:在Rt△ABC中,∠C=90°,若∠A≠45°,所以AC≠BC.
证明:假设AC=BC,∵∠A≠45°,∠C=90°,∴∠A≠∠B,∴AC≠BC.这与假设矛盾,所以AC≠BC.
上面的证明有没有错误?若没有错误,指出其证明的方法;若有错误,请予以纠正.

