2022-2023学年冀教版数学八上期末复习专题7 等腰三角形
试卷更新日期：2022-11-24 类型：复习试卷
一、单选题（1-10题每题3分，11-12题每题4分，共38分）
-
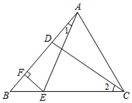
1. 若等腰三角形的周长为26cm，一边为6cm，则腰长为（ ）A、6cm B、10cm C、10cm或6cm D、以上都不对2. 若等腰三角形有一个角是40°，则它的底角为（ ）A、40° B、70° C、40°或70 D、40°或100°3. 如图，AD是等腰△ABC底边BC边上的中线，BE 平分∠ABC，交AD于点E，AC=12，DE=3，则△ABE 的面积是（ ）
A、16 B、18 C、32 D、364. 如图，已知 ， 若 ， ， ， 则下列结论不一定正确的是（ ）
A、 B、 C、 D、5. 如图，为AB的垂直平分线，则＝（ ）
A、55° B、60° C、70° D、80°6. 若一个等腰三角形的一条边是另一条边的k倍，我们把这样的等腰三角形叫做“k倍边等腰三角形”．如果一个等腰三角形是“4倍边等腰三角形”，且周长为18cm，则该等腰三角形底边长为（ ）A、12cm B、12cm或2cm C、2cm D、4cm或12cm7. 如图，CD是等腰三角形 △ABC底边上的中线，BE平分∠ABC，交CD于点E，AC＝8，DE＝2，则 △ BCE的面积是（ ）
A、4 B、6 C、8 D、128. 如图，∠BOC＝9°，点A在OB上，且OA＝1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1 ， 得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2 ， 得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3 ， 得第3条线段A2A3…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n＝（ ）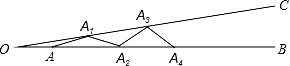
A、10 B、9 C、8 D、79. 如图， 中， ， ， 的垂直平分线分别交 于点E，F，与 ， 分别交于点D，G，则 的度数为（ ）
A、 B、 C、 D、10. 如图，直线a，b相交形成的夹角中，锐角为52°，交点为O，点A在直线a上，直线b上存在点B，使以点O，A，B为顶点的三角形是等腰三角形，这样的点B有（ ）
A、1个 B、2个 C、3个 D、4个11. 有一题目：“如图，∠ABC=40°，BD平分∠ABC ， 过点D作DE∥AB交BC于点E ， 若点F在AB上，且满足DF=DE ， 求∠DFB的度数．”小贤的解答：以D为圆心，DE长为半径画圆交AB于点F ， 连接DF ， 则DE=DF ， 由图形的对称性可得∠DFB=∠DEB ． 结合平行线的性质可求得∠DFB=140°．而小军说：“小贤考虑的不周全，∠DFB还应有另一个不同的值”．下列判断正确的是（ ）
A、小军说的对，且∠DFB的另一个值是40° B、小军说的不对，∠DFB只有140°一个值 C、小贤求的结果不对，∠DFB应该是20° D、两人都不对，∠DFB应有3个不同值12. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（ ）①△ABE的面积＝△BCE的面积；②∠FAG＝∠FCB；③AF＝AG；④BH＝CH．
A、①②③④ B、①②③ C、②④ D、①③二、解答题（共4题，共45分）
-
13. 如图，在△ABC中，AB=AC ， BD= CD ， DE⊥AB ， DF⊥AC ， 垂足分别为点E、F ， 求证：DE=DF.
14.如图， △ABC中， AB=AC ，D、E分别是AB、AC上的点，且 ∠ABE=∠ACD ，BE、CD交于点O，求证： △OBC是等腰三角形.
15. 如图，在等腰△ABC和等腰△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE且C、E、D三点共线，作AM⊥CD于M．若BD＝5，DE＝4，求CM．
16. 探究与发现：如图①，在Rt△ABC中，∠BAC=90°，AB=AC，点D在底边BC上，AE=AD，连结DE.
(1)、当∠BAD=60°时，求∠CDE的度数；(2)、当点D在BC （点B、C除外） 上运动时，试猜想并探究∠BAD与∠CDE的数量关系；(3)、深入探究：若∠BAC≠90°，试就图②探究∠BAD与∠CDE的数量关系.三、填空题（13-15题每题3分，16-17题每题4分，共17分）
-
17. 等腰三角形一腰的中垂线与另一腰所在直线夹角为40°，该等腰三角形的底角的度数是.18. 如果等腰三角形的周长是27cm，一腰上的中线把三角形分成两个三角形，其周长之差是3cm，则这个等腰三角形的底边长为cm。19. 如图，在△ABC中，AB=AC，D是BC中点，点E、F、G是线段AD上的三个点，若BC＝4cm，AD＝6cm，则图中阴影部分的面积为cm2 ．
