2022-2023学年冀教版数学八上期末复习专题8 直角三角形和勾股定理
试卷更新日期：2022-11-24 类型：复习试卷
一、单选题（每题3分，共36分）
-
1. 已知的两条高线交于点 ， 若 ， 则的度数为（ ）A、 B、 C、或 D、或2. 如图，在△ABC中，∠BAC=90°，AB=8，AC=6，点D为 BC 的中点，则AD 的长为（ ）
A、4.8 B、5 C、6 D、83. 已知等边△ABC的边长为12， D是边AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G.当G与D重合时，AD的长是（ ）A、3 B、4 C、8 D、94. 如图，某社会实践学习小组为测量学校A与河对岸江景房B之间的距离，在学校附近选一点C，利用测量仪器测得 ， ， AC=300米．由此可求得学校与江景房之间的距离等于
A、150米 B、600米 C、800米 D、1200米5. 我们称网格线的交点为格点．如图，在4×4的长方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，则满足条件的格点C的个数是（ ）
A、3 B、4 C、5 D、66. 直角三角形两直角边长度为5，12，则斜边上的高（ ）A、6 B、8 C、13 D、7. 如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，分别以AC，BC，AB为一边在△ABC外面做三个正方形，记三个正方形的面积依次为 ， ， ． 已知 ， 则为（ ）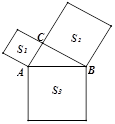
A、18 B、27 C、36 D、458. 已知：如图，在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°.
其中正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个9. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（ ）A、 B、∠A＝∠B+∠C C、∠A：∠B：∠C＝3：4：5 D、a＝6，b＝8，c＝1010. 如图，长方体的高为 ， 底面是边长为的正方形一只蚂蚁从顶点开始爬向顶点 ， 那么它爬行的最短路程为（ ）
A、 B、 C、 D、11. 如图，以 的三边为直角边分别向外作等腰直角三角形.若 ，则图中阴影部分的面积为（ ）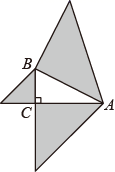
A、3 B、 C、 D、12. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用 、 表示直角三角形的两直角边 ，下列四个说法：① ，② ，③ ，④ ．其中说法正确的是（ ）
A、①③ B、①②③ C、①②④ D、①②③④二、填空题（每题3分，共18分）
-
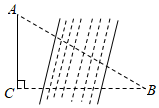
13. 如图，某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离，在学校附近选一点C，利用测量仪器测得∠A＝60°，∠C＝90°，AC＝1km.据此，可求得学校与水上乐园之间的距离AB等于 km.
14. 如图，在中，∠ACB=90°，∠B=15°，点D为AB中点，DE⊥AB交BC于点E，BE=8cm，则AC=cm．
15. 将一副三角尺如图所示叠放在一起，若AB＝4cm，则阴影部分的面积是cm2 ．
16. 如图，把两块大小相同的含45°的三角板ACF和三角板CFB如图所示摆放，点D在边AC上，点E在边BC上，且∠CFE＝13°，∠CFD＝32°，则∠DEC的度数为 ．
17. 在Rt△ABC中，AC＝8，BC＝6，∠C＝90°．现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则DE的长为 ．
18. 如图在直线上一次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1，2，3，正放置的四个正方形的面积依次是S1 ， S2 ， S3 ， S4 ， 则S1＋2S2＋2S3＋S4= ．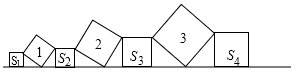
三、解答题（共4题，共46分）
