2023年春季湘教版数学九年级下册第三章 《投影与视图》单元检测A
试卷更新日期：2022-11-24 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 下列投影现象属于平行投影的是（ ）A、手电筒发出的光线所形成的投影 B、太阳光发出的光线所形成的投影 C、路灯发出的光线所形成的投影 D、台灯发出的光线所形成的投影2. 三角尺在灯泡O的照射下在墙上形成的影子如图所示，OA＝20cm，OA′＝50cm，则这个三角尺的周长与它在墙上形成的影子的周长的比是（ ）
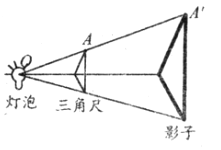A、5：2 B、2：5 C、4：25 D、25：43. 赤峰市某青少年宫门前有一座正方体雕塑，它的每个面上都有一个汉字，如图是该正方体模型的展开图，那么在正方体中，与“英”字所在面相对的面上的汉字是（ ）
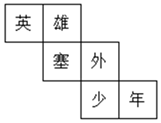A、塞 B、外 C、少 D、年4. 将如图的正方形沿图中粗黑的棱剪开，把它展开成平面图形， 则图中的线段AB与CD在展开图中，它们所在的直线之间的位置关系（ ）
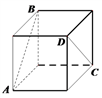A、平行 B、垂直 C、相交成60°角 D、相交成45°角5. 如果圆柱底面直径为6cm，母线长为4cm，那么圆柱的侧面积为（ ）A、24πcm2 B、36πcm2 C、12πcm2 D、48πcm26. 如图，晚上小亮在路灯下散步，他从A处向着路灯灯柱方向径直走到B处，这一过程中他在该路灯灯光下的影子( )
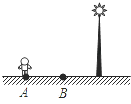A、逐渐变短 B、逐渐变长 C、先变短后变长 D、先变长后变短7. 如图，下面每一组图形都由四个等边三角形组成，其中可以折叠成三棱锥的是（ ）
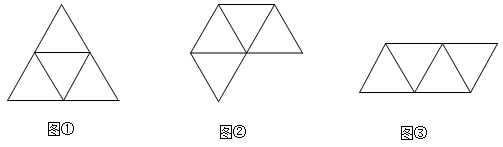A、仅图① B、图①和图② C、图②和图③ D、图①和图③8. 如图是某工件的三视图，则此工件的表面积为（ ）
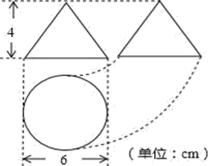A、cm2 B、cm2 C、cm2 D、cm29. 已知某几何体的三视图(单位：cm)如图所示，则该几何体的体积是（ ）
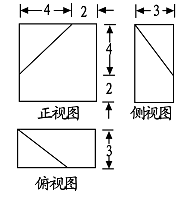A、108cm3 B、100 cm3 C、92cm3 D、84cm310.一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（ ）
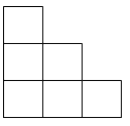A、7种 B、8种 C、9种 D、10种二、填空题（每空3分，共18分）
-
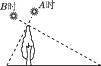
11. 如图，林林在A时测得某树的影长为2 m，B时又测得该树的影长为8 m，若两次日照的光线互相垂直，则该树的高度为
12. 如图是一幢建筑物和一根旗杆在一天中四个不同时刻的影子．将四幅图按先后顺序排列应为 ．
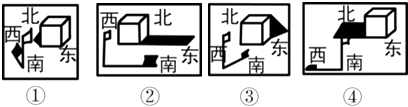13. 有如图四张卡片，除卡片上的图案不同其余完全相同，现把这些卡片有图案的一面朝下搅匀，随机抽出一张，上面的图案能够围成一个正方体的概率是.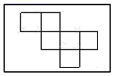
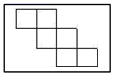
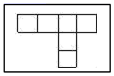
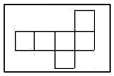14. 如图是一个正方体的表面展开图，还原成正方体后，标注了字母A的面是正方体的正面，若正方体的左面与右面所标注代数式的值相等，则x的值是.
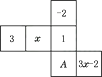15. 如图，是一圆锥的主视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的度数为.
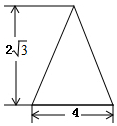16. 三棱柱的三视图如图所示，已知△EFG中，EF=8cm，EG=12cm，∠EFG=45°．则AB的长为cm．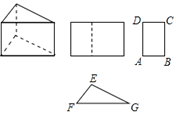
三、解答题（共8题，共72分）
-
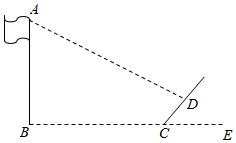
17. 如图所示，小红想利用竹竿来测量旗杆AB的高度，在某一时刻测得1米长的竹竿竖直放置时影长2米，在同时刻测量旗杆的影长时，旗杆的影子一部分落在地面上（BC），另一部分落在斜坡上（CD），他测得落在地面上的影长为10米，落在斜坡上的影长为4 米，∠DCE＝45°，求旗杆AB的高度？
18.一张宽为6cm的平行四边形纸带ABCD如图1所示，AB=10cm，小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴（要求包贴时没有重叠部分）．小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析．
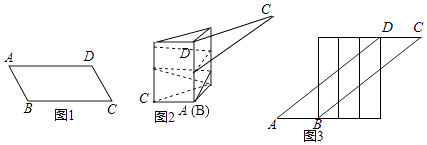(1)、若纸带在侧面缠绕三圈，正好将这个直三棱柱纸盒的侧面全部包贴满．则纸带AD的长度为 cm；(2)、若AD=100cm，纸带在侧面缠绕多圈，正好将这个直三棱柱纸盒的侧面全部包贴满．则这个直三棱柱纸盒的高度是 cm．19. 如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）．已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x（cm）．
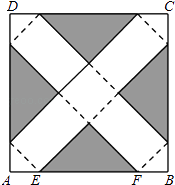(1)、若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；(2)、某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？20. 如图是一个几何体的三视图．
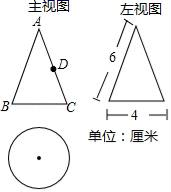(1)、写出这个几何体的名称；(2)、根据所示数据计算这个几何体的表面积．21. 如图，某人在山坡坡脚 处测得一座建筑物顶点 的仰角为 ，沿山坡向上走到 处再测得该建筑物顶点 的仰角为 .已知 米， ， 的延长线交于点 ，山坡坡度为 （即 ）.注：取 为 .
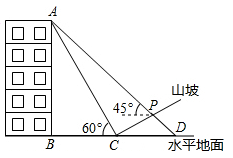(1)、求该建筑物的高度（即 的长）.(2)、求此人所在位置点 的铅直高度（测倾器的高度忽略不计）.(3)、若某一时刻， 米长木棒竖放时，在太阳光线下的水平影长是 米，则同一时刻该座建筑物顶点 投影与山坡上点 重合，求点 到该座建筑物的水平距离.22. 在阳光下，小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米，同时小强同学测量树的高度时，发现树的影子有一部分0.2米落在教学楼的第一级台阶上，落在地面上的影长为4.42米，每级台阶高为0.3米．小玲说：“要是没有台阶遮挡的话，树的影子长度应该是4.62米”；小强说：“要是没有台阶遮挡的话，树的影子长度肯定比4.62米要长”．
(1)、你认为小玲和小强的说法对吗？(2)、请根据小玲和小强的测量数据计算树的高度；(3)、要是没有台阶遮挡的话，树的影子长度是多少？23. 有两张长12cm，宽10cm的矩形纸板，分别按照图1与图2两种方式裁去若干小正方形和小矩形，剩余部分（阴影部分）恰好做成无盖和有盖的长方体纸盒各一个.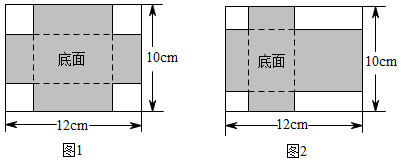
(1)、做成有盖长方体纸盒的裁剪方式是（填“图1”或“图2”）.(2)、已知图1中裁去的小正方形边长为1.5cm，求做成的纸盒的底面积.(3)、已知按图2裁剪方式做成纸盒的底面积为24cm2 ， 则剪去的小正方形的边长为多少cm？24. 空间任意选定一点O，以点O为端点，作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴，统称为坐标轴，它们的方向分别为ox（水平向前）、oy（水平向右）、oz（竖直向上）方向，这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为S1、S2、S3 ， 且S1＜S2＜S3的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体S1所在的面与x轴垂直，S2所在的面与y轴垂直，S3所在的面与z轴垂直，如图1所示.
若将x轴方向表示的量称为几何体码放的排数，y轴方向表示的量称为几何体码放的列数，z轴方向表示的量称为几何体码放的层数；如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了1排2列6层，用有序数组记作（1，2，6），如图3的几何体码放了2排3列4层，用有序数组记作（2，3，4）.这样我们就可用每一个有序数组（x，y，z）表示一种几何体的码放方式.
(1)、如图是由若干个单位长方体码放的一个几何体的三视图，写出这种码放方式的有序数组，组成这个几何体的单位长方体的个数为多少个；
(2)、对有序数组性质的理解，下列说法正确的是哪些；（只写序号）①每一个有序数组（x，y，z）表示一种几何体的码放方式.
②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数.
③有序数组不同，所表示几何体的单位长方体个数不同.
④不同的有序数组所表示的几何体的体积不同.
⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S1、S2、S3的个数.
(3)、为了进一步探究有序数组（x，y，z）的几何体的表面积公式S（x，y，z） ， 某同学针对若干个单位长方体进行码放，制作了下列表格：几何体
有序数组
单位长方体的个数
表面上面积为 的个数
表面上面积为 的个数
表面上面积为 的个数
表面积
(1，1，1)
1
2
2
2
2S1+2S2+2S3
(1，2，1)
2
4
2
4
4S1+2S2+4S3
(3，1，1)
3
2
6
6
2S1+6S2+6S3
(2，1，2)
4
4
8
4
4S1+8S2+4S3
(1，5，1)
5
10
2
10
10S1+2S2+10S3
(1，2，3)
6
12
6
4
12S1+6S2+4S3
(1，1，7)
7
14
14
2
14S1+14S2+2S3
(2，2，2)
8
8
8
8
8S1+8S2+8S3
…
…
…
…
…
…
根据以上规律，请写出有序数组（x，y，z）的几何体表面积计算公式S（x，y，z）；（用x、y、z、S1、S2、S3表示）
(4)、当S1=2，S2=3，S3=4时，对由12个单位长方体码放的几何体进行打包，为了节约外包装材料，对12个单位长方体码放的几何体表面积最小的规律进行探究，根据探究的结果请写出使几何体表面积最小的有序数组，并用几何体表面积公式求出这个最小面积.（缝隙不计）