2023年春季湘教版数学九年级下册第二章 《圆》单元检测B
试卷更新日期:2022-11-23 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,是的两条半径,点C在上,若 , 则的度数为( )
 A、 B、 C、 D、2. 如图,已知 , 点为边上一点, , 点为线段的中点,以点为圆心,线段长为半径作弧,交于点 , 连接 , 则的长是( )
A、 B、 C、 D、2. 如图,已知 , 点为边上一点, , 点为线段的中点,以点为圆心,线段长为半径作弧,交于点 , 连接 , 则的长是( )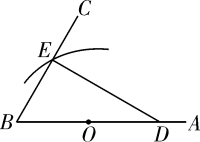 A、5 B、 C、 D、3. 如图,内接于 , AD是的直径,若 , 则的度数是( )
A、5 B、 C、 D、3. 如图,内接于 , AD是的直径,若 , 则的度数是( ) A、60° B、65° C、70° D、75°4. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( )
A、60° B、65° C、70° D、75°4. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( )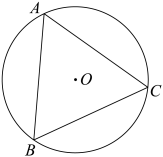 A、 B、 C、 D、5. 如图所示,等边的顶点在⊙上,边、与⊙分别交于点、 , 点是劣弧上一点,且与、不重合,连接、 , 则的度数为( )
A、 B、 C、 D、5. 如图所示,等边的顶点在⊙上,边、与⊙分别交于点、 , 点是劣弧上一点,且与、不重合,连接、 , 则的度数为( ) A、 B、 C、 D、6. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、57. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2 m,则改建后门洞的圆弧长是( )
A、 B、 C、 D、6. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、57. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2 m,则改建后门洞的圆弧长是( ) A、 m B、 m C、 m D、( +2)m8. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A、 m B、 m C、 m D、( +2)m8. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )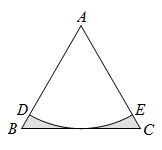 A、 B、 C、 D、9. 如图,在中, , , , 以点为圆心,的长为半径画弧,交于点 , 则的长为( )
A、 B、 C、 D、9. 如图,在中, , , , 以点为圆心,的长为半径画弧,交于点 , 则的长为( )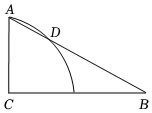 A、 B、 C、 D、10. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )
A、 B、 C、 D、10. 如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )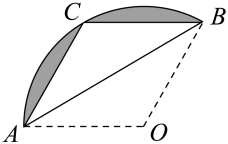 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图,点 , , 在 上, ,则 的度数是
 12. 如图,在半径为1的上顺次取点 , , , , , 连接 , , , , , . 若 , , 则与的长度之和为 . (结果保留).
12. 如图,在半径为1的上顺次取点 , , , , , 连接 , , , , , . 若 , , 则与的长度之和为 . (结果保留). 13. 如图,是的直径,点、在上, , 则度.
13. 如图,是的直径,点、在上, , 则度. 14. 如图,在平面直角坐标系中,点的坐标为 , 点在轴正半轴上,以点为圆心,长为半径作弧,交轴正半轴于点 , 则点的坐标为 .
14. 如图,在平面直角坐标系中,点的坐标为 , 点在轴正半轴上,以点为圆心,长为半径作弧,交轴正半轴于点 , 则点的坐标为 .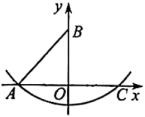 15. 如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为cm(玻璃瓶厚度忽略不计).
15. 如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20cm,底面直径BC=12cm,球的最高点到瓶底面的距离为32cm,则球的半径为cm(玻璃瓶厚度忽略不计). 16. 如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为cm.
16. 如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为cm.
三、解答题(共8题,共72分)
-
17. 如图,在中,为的直径,点E在上,D为的中点,连接并延长交于点C.连接 , 在的延长线上取一点F,连接 , 使 .
 (1)、求证:为的切线;(2)、若 , 求的半径.18. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .
(1)、求证:为的切线;(2)、若 , 求的半径.18. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .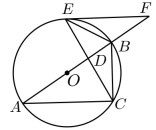 (1)、求证:是的切线.(2)、若 , , 求的半径.19. 如图,是的直径,是的一条弦,连接
(1)、求证:是的切线.(2)、若 , , 求的半径.19. 如图,是的直径,是的一条弦,连接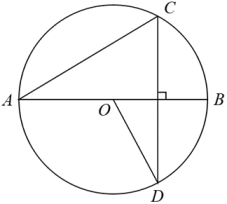 (1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.20. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.
(1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.20. 如图,D是以AB为直径的⊙O上一点,过点D的切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C,垂足为点F.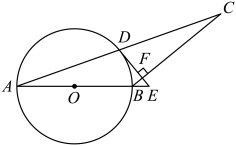 (1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.21.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);
(1)、求证:AB=CB;(2)、若AB=18,sinA= , 求EF的长.21.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);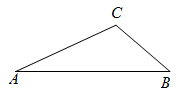 (2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.
(2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.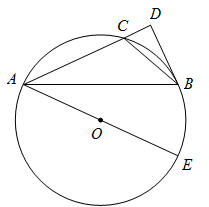
①求证:;
②若 , , 求的半径.
22. 如图,已知是的角平分线,点是斜边上的动点,以点为圆心,长为半径的经过点 , 与相交于点. (1)、判定与的位置关系,为什么?(2)、若 , ,
(1)、判定与的位置关系,为什么?(2)、若 , ,①求、的值;
②试用和表示 , 猜测与 , 的关系,并用给予验证.

