2023年春季湘教版数学九年级下册第二章 《圆》单元检测A
试卷更新日期:2022-11-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( )
 A、相切 B、相交 C、相离 D、平行2. 如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若 , 则的度数是( )
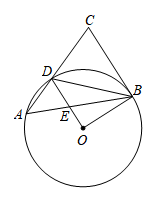
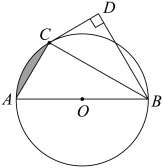
A、相切 B、相交 C、相离 D、平行2. 如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若 , 则的度数是( )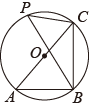 A、 B、 C、 D、3. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
A、 B、 C、 D、3. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
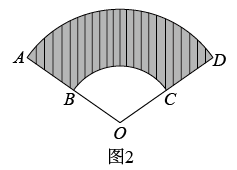 A、 B、 C、 D、4. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )
A、 B、 C、 D、4. 如图,在中, , , . 以点为圆心,为半径作圆,当点在内且点在外时,的值可能是( )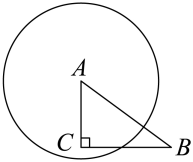 A、2 B、3 C、4 D、55. 如图,为的直径,弦交于点 , , , , 则( )
A、2 B、3 C、4 D、55. 如图,为的直径,弦交于点 , , , , 则( )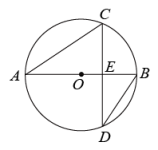 A、 B、 C、1 D、26. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
A、 B、 C、1 D、26. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、7. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )
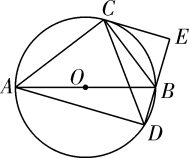
A、 B、 C、 D、7. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )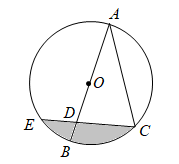 A、 B、 C、 D、8. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )
A、 B、 C、 D、8. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )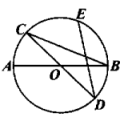 A、 B、 C、 D、9. 如图,正六边形ABCDEF内接于⊙O,半径为6,则这个正六边形的边心距OM和的长分别为( )
A、 B、 C、 D、9. 如图,正六边形ABCDEF内接于⊙O,半径为6,则这个正六边形的边心距OM和的长分别为( )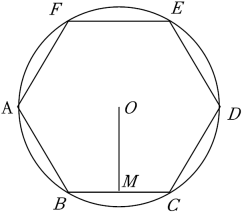 A、4, B、3 , π C、2 , D、3 , 2π10. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )
A、4, B、3 , π C、2 , D、3 , 2π10. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )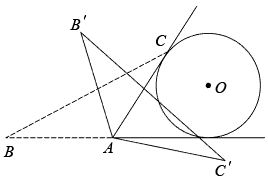 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每空3分,共18分)
-
11. 如图,在中,AB是的弦,的半径为3cm,C为上一点, , 则AB的长为cm.
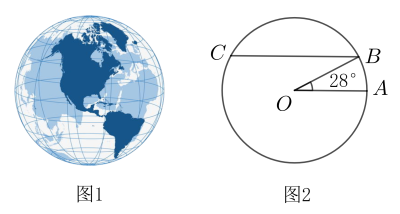
 12. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.
12. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径约为6400千米,弦 , 以为直径的圆的周长就是北纬28°纬线的长度;(参考数据: , , , )
根据以上信息,北纬28°纬线的长度约为千米.
 13. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .
13. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .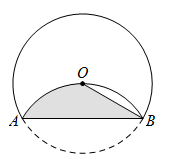 14. 如图,⊙O的直径AB经过弦CD的中点H,若cos∠CDB= ,BD=5,则⊙O的半径为 .
14. 如图,⊙O的直径AB经过弦CD的中点H,若cos∠CDB= ,BD=5,则⊙O的半径为 .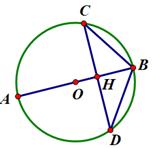 15. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
15. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.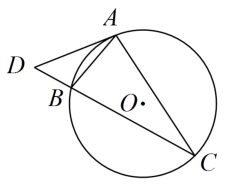 16. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.
16. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.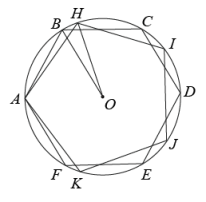
三、解答题(共8题,共72分)
-
17. 如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D.
 (1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.18. 是的直径,C是上一点, , 垂足为D,过点A作的切线,与的延长线相交于点E.
(1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.18. 是的直径,C是上一点, , 垂足为D,过点A作的切线,与的延长线相交于点E.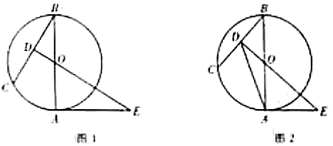 (1)、如图1,求证;(2)、如图2,连接 , 若的半径为2, , 求的长.19. 如图,点O是的边AC上一点,以点O为圆心,OA为半径作 , 与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F, .
(1)、如图1,求证;(2)、如图2,连接 , 若的半径为2, , 求的长.19. 如图,点O是的边AC上一点,以点O为圆心,OA为半径作 , 与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F, .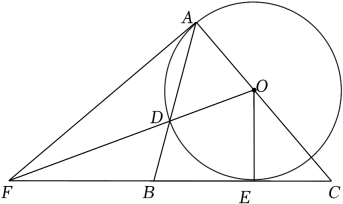 (1)、连接AF,求证:AF是的切线;(2)、若 , , 求FD的长.20. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 .
(1)、连接AF,求证:AF是的切线;(2)、若 , , 求FD的长.20. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 . (1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.21. (现有若干张相同的半圆形纸片,点是圆心,直径的长是 , 是半圆弧上的一点(点与点、不重合),连接、.
(1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.21. (现有若干张相同的半圆形纸片,点是圆心,直径的长是 , 是半圆弧上的一点(点与点、不重合),连接、.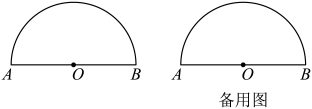 (1)、沿、剪下 , 则是三角形(填“锐角”、“直角”或“钝角”);(2)、分别取半圆弧上的点、和直径上的点、.已知剪下的由这四个点顺次连接构成的四边形是一个边长为的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);(3)、经过数次探索,小明猜想,对于半圆弧上的任意一点 , 一定存在线段上的点、线段上的点和直径上的点、 , 使得由这四个点顺次连接构成的四边形是一个边长为的菱形.小明的猜想是否正确?请说明理由.
(1)、沿、剪下 , 则是三角形(填“锐角”、“直角”或“钝角”);(2)、分别取半圆弧上的点、和直径上的点、.已知剪下的由这四个点顺次连接构成的四边形是一个边长为的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);(3)、经过数次探索,小明猜想,对于半圆弧上的任意一点 , 一定存在线段上的点、线段上的点和直径上的点、 , 使得由这四个点顺次连接构成的四边形是一个边长为的菱形.小明的猜想是否正确?请说明理由.