沪科版数学2022~2023学年初三数学一轮复习模拟卷(一)
试卷更新日期:2022-11-22 类型:一轮复习
一、单选题(每题4分,共40分)
-
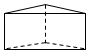
1. 实数中, 最小的数是( )A、 B、0 C、 D、22. 下列运算正确的是A、 B、 C、 D、3. 2022年北京冬奥会全冰面速滑馆为亚洲之最,它的冰面面积约为12000平方米,数据12000用科学记数法表示为( )A、 B、 C、 D、4. 一个几何体如图水平放置,它的主视图是( )
 A、
A、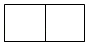 B、
B、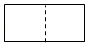 C、
C、 D、
D、 5. 如图,数轴上点A,B分别对应2,4,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C;以原点O为圆心, 长为半径画弧,交数轴于点M,则点M对应的数是( )
5. 如图,数轴上点A,B分别对应2,4,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C;以原点O为圆心, 长为半径画弧,交数轴于点M,则点M对应的数是( )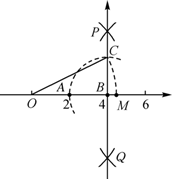 A、 B、 C、5 D、6. 如图,已知点A,B,C依次在⊙o上,∠B-∠A=40°,则∠AOB的度数为( )
A、 B、 C、5 D、6. 如图,已知点A,B,C依次在⊙o上,∠B-∠A=40°,则∠AOB的度数为( )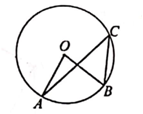 A、84° B、80° C、72° D、70°7. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则正确的方程是( )A、 B、 C、 D、8. 甲、乙两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,符合这一结果的试验可能是( )
A、84° B、80° C、72° D、70°7. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则正确的方程是( )A、 B、 C、 D、8. 甲、乙两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,符合这一结果的试验可能是( ) A、抛一枚硬币,出现正面的概率 B、任意写一个正整数,它能被3整除的概率 C、从一装有1个白球和2个红球的袋子中任取一球,取到红球的概率 D、掷一枚正方体的骰子,出现 6 点的概率9. 如图,中, , , , 将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为( )
A、抛一枚硬币,出现正面的概率 B、任意写一个正整数,它能被3整除的概率 C、从一装有1个白球和2个红球的袋子中任取一球,取到红球的概率 D、掷一枚正方体的骰子,出现 6 点的概率9. 如图,中, , , , 将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共20分)
-
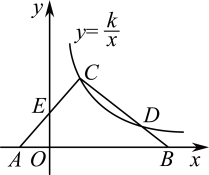
11. 已知x,y为实数,且 , 则的立方根是 .12. 因式分解: .13. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
 14. 新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2﹣x+c(c为常数)在﹣2<x<4的图象上存在两个二倍点,则c的取值范围是 .
14. 新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2﹣x+c(c为常数)在﹣2<x<4的图象上存在两个二倍点,则c的取值范围是 .三、综合题(共9题,共90分)
-
15. 先化简,再求值 , 其中16. 在平面直角坐标系中,各顶点的坐标分别为 , , .
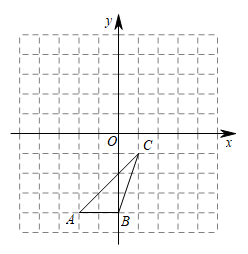 (1)、请在图中画出绕点逆时针旋转90°后的图形 , 并写出各顶点的坐标;(2)、请在图中画出绕点顺时针旋转180°后的图形.17. 如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)、请在图中画出绕点逆时针旋转90°后的图形 , 并写出各顶点的坐标;(2)、请在图中画出绕点顺时针旋转180°后的图形.17. 如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.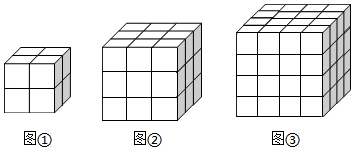 (1)、第1个几何体中只有2个面涂色的小立方体共有个;第2个几何体中只有2个面涂色的小立方体共有个;第3个几何体中只有2个面涂色的小立方体共有个.(2)、求出第10个几何体中只有2个面涂色的小立方体的块数.(3)、求出前100个几何体中只有2个面涂色的小立方体的块数的和.18. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由改为已知原传送带长为
(1)、第1个几何体中只有2个面涂色的小立方体共有个;第2个几何体中只有2个面涂色的小立方体共有个;第3个几何体中只有2个面涂色的小立方体共有个.(2)、求出第10个几何体中只有2个面涂色的小立方体的块数.(3)、求出前100个几何体中只有2个面涂色的小立方体的块数的和.18. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由改为已知原传送带长为 (1)、求新传送带的长度;(2)、如果需要在货物着地点的右侧留出的通道,试判断距离点的货物是否需要挪走,并说明理由.19. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
(1)、求新传送带的长度;(2)、如果需要在货物着地点的右侧留出的通道,试判断距离点的货物是否需要挪走,并说明理由.19. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .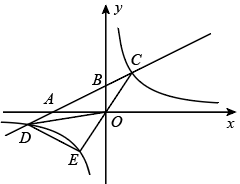 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.20. 如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.20. 如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.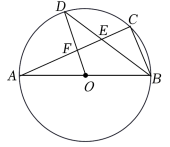 (1)、求证:点D为的中点;(2)、若DF=4,AC=16,求⊙O的直径.21. 为了解全校学生上学的交通方式,该校九年级(8)班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2.根据以上信息,解答下列问题:
(1)、求证:点D为的中点;(2)、若DF=4,AC=16,求⊙O的直径.21. 为了解全校学生上学的交通方式,该校九年级(8)班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选,并将调查结果绘制成条形统计图1和扇形统计图2.根据以上信息,解答下列问题: (1)、本次接受调查的总人数是 ▲ 人,并把条形统计图补充完整;(2)、在扇形统计图中,“乘私家车”的人数所占的百分比是 , “其他方式”所在扇形的圆心角度数是度;(3)、已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好都是女生的概率.22. 某服装店销售A、B两种服装,它们的进价和售价如下表,若老板进A种服装20套和B种服装30套,则需资金18000元;若老板进A种服装30套和B种服装40套,则需要资金25000元.
(1)、本次接受调查的总人数是 ▲ 人,并把条形统计图补充完整;(2)、在扇形统计图中,“乘私家车”的人数所占的百分比是 , “其他方式”所在扇形的圆心角度数是度;(3)、已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果,请你用列表法或画树状图的方法,求出恰好都是女生的概率.22. 某服装店销售A、B两种服装,它们的进价和售价如下表,若老板进A种服装20套和B种服装30套,则需资金18000元;若老板进A种服装30套和B种服装40套,则需要资金25000元.种类
A
B
进价(元/套)
a
b
售价(元/套)
480
660
(1)、求A、B两种衣服每套的进价;(2)、若老板用不超过36000元的资金进A、B两种服装共100套,则老板按售价卖出这100套服装的最大利润是多少?(3)、根据市场情况,老板在11月份按售价可卖A种服装14套.假设老板按售价每套A种服装每降价10元,就可多卖出一套A种服装,请问当售价定为多少时,老板在11月份卖A种服装获得的利润最大.23. 如图,在正方形中,点是边上的一点不与重合 , 将线段 绕点顺时针旋转得到线段 , 连接 , 与边交于点 , 与相交于点 . (1)、求证:;(2)、当平分时,求证:;(3)、当 时,求的值.
(1)、求证:;(2)、当平分时,求证:;(3)、当 时,求的值.