浙江省湖州市吴兴区2022-2023学年八年级上学期数学期中试卷
试卷更新日期：2022-11-22 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组线段，能组成三角形的是（ ）A、2，3，4 B、1，2，3 C、3，4，9 D、15，12，23. 已知图中的两个三角形全等，则∠1等于（ ）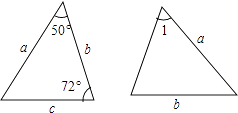
A、72° B、60° C、50° D、58°4. 等腰三角形的两边长分别为4cm和8cm，则它的周长为（ ）A、16cm B、17cm C、20cm D、16cm或20cm5. 如图，OP平分∠AOB ， PC⊥OA于C ， 点D是OB上的动点，若PC＝6cm ， 则PD的长可以是（ ）
A、7cm B、4cm C、5cm D、3cm6. 若x＞y，则下列式子错误的是（ ）A、x-3＞y-3 B、-3x＞-3y C、x+3＞y+3 D、7. 如图，DE 是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（ ）
A、16 B、18 C、26 D、288. 如图， ， ，要使 ，需添加一个条件，下列所给的条件及相应的判定定理不正确的是（ ）
A、 B、 C、 D、9. 如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD．若CD=AC，∠A=50°，则∠ACB的度数为（ ）
A、 B、 C、 D、10. 如图，△AOB≌△ADC，点B和点C是对应顶点，∠O＝∠D＝90°，记∠OAD＝α，∠ABO＝β，当BC∥OA时，α与β之间的数量关系为（ ）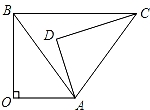
A、α＝β B、α＝2β C、α+β＝90° D、α+2β＝180°二、填空题（本题有6小题，每小题4分，共24分）
-
11. 命题“相等的角是对顶角”是命题（填“真”或“假”）12. 三角形的两边长分别是10和8，则第三边x的取值范围是 ．13. 已知等腰三角形的顶角是底角的4倍，则顶角的度数为°．14. 如图，在中，斜边上的中线CD=5，则 ．
15. 如图，在Rt△ABC中，∠C=90°，∠A=30°，BD=2CD，则∠ADB=度．
16. 如图，在矩形ABCD中，AB＝3，AD＝4，E、F分别边BC、CD上一点，EF⊥AE，将△ECF沿EF翻折得△EC′F，连接AC′，当BE＝时，△AEC′是以AE为腰的等腰三角形．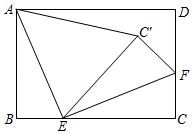
三、解答题（本题有8小题，共66分）
-
17. 若x＜y，且（a-3）x＞（a-3）y，求a的取值范围.18. 如图，每个小正方形的边长都为1．求四边形ABCD的周长及面积．
19. 如图，AB=AC，AD=AE，∠1=∠2，求证：∠B=∠C．
20. 如图，在等边三角形中，D是上的一点，E是延长线上一点，连接、 ， 已知 ．
(1)、求证：是等腰三角形(2)、当 ， 时，求的面积．21. 如图，在△ABC中，∠BAC＝90°，AB＝AC，D是AC边上一点，连接BD，EC⊥AC，且AE＝BD，AE与BC交于点F．
(1)、求证：△ABD≌△CAE；(2)、当AD＝CF时，求∠ABD的度数．22. 如图，△ABC中，CD、BE分别是高，M、N分别是线段BC、DE的中点．求证：MN⊥DE.
23. 八（1）班小明和小亮同学学习了“勾股定理”之后，为了测得下图风筝CE的高度，他们进行了如下操作：①测得BD的长度为24米；
②根据手中剩余线的长度计算出风筝线BC的长为30米；
③牵线放风筝的小明身高AB为1.68米．
(1)、求风筝的高度CE；(2)、若小亮让风筝沿CD方向下降了8米到点M（即CM=8米），则他往回收线多少米？24. 【概念认识】如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．
(1)、【问题解决】
如图②，在△ABC中，∠A＝80°，∠B＝45°，若∠B的三分线BD交AC于点D，求∠BDC的度数；(2)、如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC＝140°，求∠A的度数；(3)、【延伸推广】
在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝m°（m＞54），∠B＝54°，直接写出∠BPC的度数．（用含m的代数式表示）