浙江省金华市义乌市苏溪、佛堂、后宅2022-2023学年九年级上学期数学期中联考试题

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 若 $\frac{b}{a} = \frac{3}{2}$ ，则 $\frac{a + b}{a}$ 的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{5}{2}$ C、 $\frac{5}{3}$ D、 $\frac{5}{4}$

查看试题解析
2. 下列语句所描述的事件中，是不可能事件的是（）

A、一岁一枯荣 B、黄河入海流 C、明月松间照 D、白发三千丈

查看试题解析
3. ⊙O的半径为 $6cm$ ，点 $A$ 到圆心 $O$ 的距离 $O A = 5 cm$ ，则点 $A$ 与⊙ $O$ 的位置关系为（）

A、点 $A$ 在圆内 B、点 $A$ 在圆上 C、点 $A$ 在圆外 D、无法确定

查看试题解析
4. 若两个相似三角形的面积之比为1：4，则它们的最长边的比是（）

A、1：2 B、1：4 C、1：16 D、无法确定

查看试题解析
5. 下列有关圆的一些结论：①平分弦的直径垂直于弦；②三点确定一个圆；③平分弧的直径垂直于弧所对的弦；④同弧或等弧所对的弦相等，其中正确的有（）

A、①③ B、②③④ C、③④ D、①③④

查看试题解析
6. 已知抛物线 $y = x^{2} - 2 x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $m^{2} - 2 m + 2021$ 的值为（）

A、2021 B、2020 C、2022 D、2023

查看试题解析
7. 如图，AB为⊙O的弦，半径OC⊥AB于点D ，且AB=6，OD=4，则DC的长为（）

A、1 B、2 C、2.5 D、5

查看试题解析
8. 如图，在▱ABCD中，Q是CD上的点，AQ交BD于点P，交BC的延长线于点R，若DQ：CQ＝3：1，则AP：PR＝（）

A、4：3 B、4：7 C、3：4 D、3：7

查看试题解析
9. 已知点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 均在抛物线 $y = a x^{2} - 2 a x + 4 (a \neq 0)$ 上，若 $x_{1} < x_{2}$ ， $x_{1} + x_{2} = 1 + a$ ，则（）

A、当 $a > 1$ 时， $y_{1} > y_{2}$ B、当 $a > 1$ 时， $y_{1} < y_{2}$ C、当 $a < 1$ 时， $y_{1} < y_{2}$ D、当 $a < 1$ 时， $y_{1} > y_{2}$

查看试题解析
10. 如图，矩形A₁B₁C₁D₁在矩形ABCD的内部，且B₁C₁⊥BC，点B₁ ， D₁在对角线BD的异侧．连结BB₁ ， DB₁ ， BD₁ ， DD₁ ，若矩形ABCD∼矩形A₁B₁C₁D₁ ，且两个矩形的周长已知．只需要知道下列哪个值就一定可以求得四边形B₁BD₁D的面积（）

A、矩形ABCD的面积 B、∠B₁BD₁的度数 C、四边形B₁BD₁D的周长 D、BB₁的长度

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 已知线段a＝2，b＝8，则线段a、b的比例中项等于．

查看试题解析
12. 林业局要考察一种树苗移植的成活率，对该市这种树苗移植成活情况进行了调查统计，并绘制了统计图，根据统计图提供的信息，估计该树苗成活的概率为．

查看试题解析
13. 如图，AB是⊙O的直径，D，C是弧BE的三等分点，∠COD=32°，则∠E的度数是．

查看试题解析
14. 如图，直线y＝kx+b与抛物线y＝-x²+2x+3交于点A，B，且点A在y轴上，点B在x轴上，则不等式-x²+2x+3＞kx+b的解集为．

查看试题解析
15. 如图， $△ ABC$ 是等边三角形， $A B = 3$ ，点 $D$ 为边 $B C$ 上的动点， $∠ A D E = 60 °$ ， $D E$ 交 $A C$ 于点 $E$ ，线段 $C E$ 的最大值为．

查看试题解析
16. 乐乐用一张直角三角形纸片玩折纸游戏．如图1，在Rt $△ ABC$ 中， $∠ A B C = 90 °$ ， $∠ A = 30 °$ ， $B C = 2$ ．第一步，将纸片沿AB对折，使点A与点B重合，折痕与边AB的交点为点D；第二步，在AC边上找一点E，将纸片沿ED折叠，点A落在 $A^{'}$ 处，如图2；第三步，将纸片沿 $D A^{'}$ 折叠，点E落在 $E^{'}$ 处，如图3．当点 $E^{'}$ 恰好在原直角三角形纸片的边上时，线段 $A^{'} E^{'}$ 的长为．

查看试题解析

三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分.）

17. 已知：线段a、b、c，满足 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，且a+b+c=27，求a-b+c的值．

查看试题解析
18. 截至2022年9月，我国已累计向国际社会提供约6214亿只口罩，超过62亿件防护服，100亿份检测试剂，为全世界人民抗击新冠肺炎做出了巨大贡献．“抗击新冠，人人有责”，学校组织开展主题演讲比赛．九年级某班一共有3位候选人，分别是小明、小丽和小王．

(1)、随机抽取一人参赛，求抽到小明参加比赛的概率.

(2)、任选两人参加比赛，求同时抽到小明和小丽参加比赛的概率.（画出树状图）

查看试题解析
19. 已知抛物线 $y = x^{2} - b x + c$ 经过 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ 两点．

(1)、求抛物线的表达式（用一般式表示）和顶点坐标；

(2)、当-1 $\leq$ x $\leq 4 时$ ，求y的取值范围.

查看试题解析
20. 如图，在7×4方格纸中，点A，B，C都在格点上，用无刻度直尺作图．

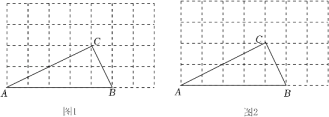(1)、在图1中的线段AC上找一个点E，使AE＝ $\frac{1}{3}$ AC；

(2)、在图2中作一个格点△CDE，使△CDE与△ABC相似．

查看试题解析
21. 如图，点A，B，C是⊙O上的三点， $A B ∥ O C$ ．

(1)、求证： $A C$ 平分 $∠ O A B$ ；

(2)、过点O作 $O E ⊥ A B$ 于点E，交 $A C$ 于点P．若 $AB = 2 \sqrt{3}$ ， $∠ AOE = 30 °$ ，求 $P E$ 的长．

查看试题解析
22. 某超市销售一种商品，每千克成本为30元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如表所示：

销售单价x（元/千克）

55

60

65

70

销售量y（千克）

70

60

50

40

(1)、求y（千克）与x（元/千克）之间的函数表达式；

(2)、为保证某天获得1600元的销售利润，则该天的销售单价应定为多少？

(3)、当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？

查看试题解析
23. 将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．

(1)、如图①，对△ABC作变换[60°， $\sqrt{3}$ ]得△AB′C′，则S_△AB′C′：S_△ABC＝；直线BC与直线B′C′所夹的锐角为度；

(2)、如图②，△ABC中，∠BAC＝30°，∠ACB＝90°，对△ABC 作变换[θ，n]得△AB′C′，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；

(3)、如图③，△ABC中，AB＝AC，∠BAC＝36°，BC＝1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

查看试题解析
24. 如图，菱形ABCD的边长为20cm，∠ABC＝120°．动点P、Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以 $2 \sqrt{3}$ cm/s的速度，沿A→C的路线向点C运动．当P、Q到达终点C时，整个运动随之结束，设运动时间为t秒．

(1)、当点P在AB上运动时，请判断PQ与对角线AC的位置关系，并说明理由；

(2)、若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．
①当t为何值时，点P、M、N在一直线上？

②当点P、M、N不在一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

查看试题解析

销售单价x（元/千克）	55	60	65	70
销售量y（千克）	70	60	50	40