浙江省宁波七中教育集团2022-2023学年八年级数上学期学期中试题

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、仔细选一选（本题有10小题，每题3分，共30分）

1. 下面是科学防控新冠知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（）

A、打喷嚏，捂口鼻 B、喷嚏后，慎揉眼 C、勤洗手，勤通风 D、戴口罩，讲卫生

查看试题解析
2. 下列长度的三段钢条，不能组成一个三角形框架的是（单位：cm）（）

A、2，3，4 B、3，7，7 C、2，2，6 D、5，6，7

查看试题解析
3. 已知a＞b，下列不等式中，不成立的是（）

A、a+4＞b+4 B、a-1＜b-1 C、5a＞5b D、-a＜-b

查看试题解析
4. 如图，在△ABC中，∠C＝90°，BD平分∠ABC，CD＝3，则点D到AB的距离是（）

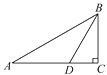A、5 B、4 C、3 D、2

查看试题解析
5. 对于命题“若a²＞b² ，则a＞b”，下面四组关于a，b的值中，能说明这个命题是假命题的是（）

A、a=-3，b=2 B、a=3，b=2 C、a=3，b=-1 D、a=-1，b=3

查看试题解析
6. 点C在x轴上方，y轴左侧，距离x轴3个单位长度，距离y轴2个单位长度，则点C的坐标为（）

A、（-3，2） B、（3，2） C、（-2，3） D、（2，3）

查看试题解析
7. 如图，O为数轴原点，A，B两点分别对应-3，3，作腰长为4的等腰△ABC，连结OC，以O为圆心，OC长为半径画弧交数轴于点M，则点M对应的实数为（）

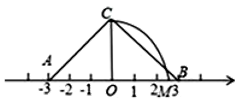A、 $\sqrt{7}$ B、4 C、 $\sqrt{5}$ D、2.5

查看试题解析
8. 把一些书分给几名同学，若每人分9本，则书本有剩余，条件* ．根据题意，设有 $x$ 名同学，可得到符合题意的不等式 $5 (x + 3) > 9 x$ ，则“条件*”可以是（）

A、每人分5本，则剩余3本 B、其中一个人分5本，则其他同学每人可分3本 C、每人分5本，则还差3本 D、每人分5本，则剩余的书可多分给3个人

查看试题解析
9. 如图，已知 △ABC和 △ADE都是等腰三角形，∠BAC=∠DAE=90° ，连结BD，CE交于点F，连结AF，下列结论：① BD=CE；② BF⊥CF；③ AF平分 ∠CAD；④ ∠AFE=45°
其中结论正确的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
10. 如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BNMC，四块阴影部分的面积分别S₁、S₂、S₃、S₄ ．则 $S_{1} - S_{2} + S {}_{3}+ S_{4}$ 等于（）

A、4 B、6 C、8 D、12

查看试题解析

二、认真填一填（本题有8小题，每题3分，共24分）

11. “x的2倍与6的和比1小”，用不等式表示为：．

查看试题解析
12. 命题“全等三角形的面积相等”的逆命题是命题．（填入“真”或“假”）

查看试题解析
13. 如图，∠B＝∠D，请添加一个条件（不另外增加字母），使得△ABC≌△ADC．你所添加的条件是．

查看试题解析
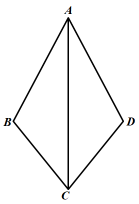14. 若直角三角形的两条直角边分别为6和8，则斜边上的中线长是．

查看试题解析
15. 在平面直角坐标系中，若点 $P (2 - m ， 7 - 2 m)$ 在第二象限，则整数m的值为．

查看试题解析
16. 已知关于x的不等式组 ${\begin{matrix} x - a \geq 0 \\ 5 - 2 x > 1 \end{matrix}$ 有解，则实数 $a$ 的取值范围是．

查看试题解析
17. 如图，已知∠MON=30°，点 $A_{1} ， A_{2} ， A_{3}$ ……在射线ON上，点 $B_{1} ， B_{2} ， B_{3}$ ……在射线OM上， $△ A_{1} B_{1} A_{2}$ 、 $△ A_{2} B_{2} A_{3}$ 、 $△ A_{3} B_{3} A_{4}$ ……均为等边三角形，若 $O A_{1} = 2$ ，则 $△ A_{2022} B_{2022} A_{2023}$ 的边长为．

查看试题解析
18. 如图，在△ABC中，AB＝AC，点D在△ABC内，AD平分∠BAC，连结CD，把△ADC沿CD折叠，AC落在CE处交AB于F，恰有CE⊥AB．若BC＝10，AD＝7，则EF＝．

查看试题解析

三、全面答一答（共6题；第19～21每题6分，第22～23每题8分，第24题12分，共46分）

19. 计算

(1)、解不等式 $5 x + 3 < 3 （ 2 + x ）$

(2)、解不等式组 ${\begin{matrix} \frac{3 x + 14}{4} > 2 x - 4 \\ 4 x + 6 \geq 3 x + 7 \end{matrix}$

查看试题解析
20. 如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C．求证：∠A=∠D．

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的顶点坐标 $A (- 1 ， 5) ， B (- 1 ， 0) ， C (- 4 ， 3)$

(1)、请在图中画出△ABC关于y轴对称的图形△ $A_{1} B_{1} C_{1}$ （其中 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 分别是A，B，C的对应点，不写画法）；

(2)、直接写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 三点的坐标：
$A_{1}$ （）， $B_{1}$ （）， $C_{1}$ （）；

(3)、在y轴上找一点P，使得PA+PB最小，这个最小值为．

查看试题解析
22. 为更好地推进生活垃圾分类工作，改善城市生态环境，某小区准备购买A、B两种型号的垃圾箱，通过对市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需390元，购买2个A型垃圾箱比购买1个B型垃圾箱少用20元．

(1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元？

(2)、该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个，且A型号垃圾箱个数不多于B型垃圾箱个数的3倍，则该小区购买A、B两种型号垃圾箱的方案有哪些？

查看试题解析
23. 如图，在△ABC中，AB=AC=2，∠A=90°.D为BC边的中点，E，F分别在AB，AC上，DE⊥DF于点D．

(1)、求证：△DEF是等腰三角形．

(2)、求EF的最小值．

查看试题解析
24. 概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．

从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

(1)、理解概念：如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，△BCD和△ACD（填“是”或者“不是”）等角三角形．

(2)、概念应用：如图2，在△ABC中，CD为角平分线，∠A=40°，∠B=60°．求证：CD为△ABC的等角分割线．

(3)、在△ABC中，∠A=42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．

查看试题解析

四、附加题（本题有3个小题，第25—26题每题3分，第27题4分，共10分）

25. 若关于x的不等式组 ${\begin{matrix} 9 x - a \geq 0 \\ 8 x - b < 0 \end{matrix}$ 的整数解为1，2，3，求适合条件的有序整数对 $(a ， b)$ 的个数．

查看试题解析
26. 周长为30，各边互不相等且都是整数的三角形共有个．

查看试题解析
27. 如图，在△ABC中，∠ABC=45°，AB= $6 \sqrt{2}$ ， AC=8，BC＞6，点E，F分别在BC，AC边上，且AF=CE，求AE+BF的最小值．

查看试题解析