浙江省杭州市观成教育集团2022-2023学年八年级上学期期中数学试卷

试卷更新日期：2022-11-22 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小四3分共30分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 下列常见的微信表情包中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下数学表达式：①4x+3y＞0；②x＝3；③x²+xy+y²；④x≠5.其中不等式有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 若a＜b，则下列结论不正确的是（）

A、a+4＜b+4 B、a-3＜b-3 C、-2a＞-2b D、 $\frac{1}{2} a > \frac{1}{2} b$

查看试题解析
4. 若三角形三个角的度数比为3：3：4，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
5. 如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，AB＝5，BD＝1，则CF的长度为（）

A、2 B、2.5 C、4 D、5

查看试题解析
6. 点P（m+3，m+1）在y轴上，则P点坐标为（）

A、（0，-2） B、（0，-4） C、（4，0） D、（2，0）

查看试题解析
7. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB，交AB于点E，DF⊥AC，交AC于点F，若DE＝2，AC＝4，则△ADC的面积是（）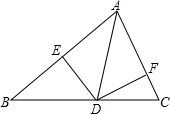

A、4 B、6 C、8 D、10

查看试题解析
8. 如图，已知长方形纸片ABCD，点E在边AB上，且BE＝2，BC＝3，将△CBE沿直线CE翻折，使点B落在点G，延长EG交CD于点F处，则线段FG的长为（）

A、 $\frac{5}{4}$ B、 $\frac{4}{3}$ C、 $\sqrt{2}$ D、1

查看试题解析
9. 如图所示，已知△ABC中，AB＝6，AC＝9，AD⊥BC于D，M为AD上任一点，则MC²-MB²等于（）

A、9 B、35 C、45 D、无法计算

查看试题解析
10. 已知等边ABC中，在射线BA上有一点D，连接CD，以CD为边向上作等边△CDE，连接BE和AE，下列结论：①∠BAE＝120°；
②当D在线段AB或BA延长线上时，总有∠BED-∠AED＝ $\frac{1}{2}$ ∠BDC.

下列说法正确的是（）

A、①②都对 B、①②都错 C、①错，②对 D、①对，②错

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分

11. 已知命题：等边三角形的各个内角都等于60.这个命题的逆命题是.

查看试题解析
12. 在平面直角坐标系中，点P（-3，2）在第象限；点P到x轴的距离是.

查看试题解析
13. 满足不等式2（2x-4）＞-3x+6的最小整数是.

查看试题解析
14. ①若ab＞0，则a＞0，b＞0；
②一个角的补角大于这个角；

③两直线平行，同位角相等；

④有两边和其中一边的对角对应相等的两个三角形全等；

⑤点P坐标为（-2，6），将其先向右平移6个单位，再向下平移8个单位，得到点P₁ ，坐标为（4，-2）.

其中是真命题的有.

查看试题解析
15. 已知 $△$ ABC 中有一个内角是30°，AB=AC，AB边上的中垂线交直线BC于点D，连结AD，则∠DAC=.

查看试题解析
16. 活动课上，小华将两张直角三角形纸片如图放置，已知AC=8， O是AC的中点，△ABO与△CDO的面积之比为4 ： 3，则OD的长度为； △OBC的面积为.

查看试题解析

三、解答题：本大题有7个小题，共66分.

17. 如图，已知∠a，∠β，线段a.用尺规求作（保留作图痕迹）：

⑴△ABC，使∠A＝∠a，∠B＝∠B，AB＝a.

⑵作△ABC中线段AB的垂直平分线.

查看试题解析
18. 解不等式（组）：

(1)、解不等式：5x-5＜2（2+x）.

(2)、解不等式组 ${\begin{array}{l} 2 x - 4 < x - 1 ① \\ \frac{3 x - 4}{6} ⩽ \frac{2 x - 1}{3} ② \end{array}$ ，并在数轴上表示该不等式组的解集.

查看试题解析
19. 如图，A，B，D依次在同一条直线上，∠A＝∠D＝∠CBE＝90°，AC＝BD.

(1)、求证：CB＝BE.

(2)、若AC＝2，AD＝6，求CE的长.

查看试题解析
20. 在平面直角坐标系中，△ABC的三个顶点分别是A（2，4），B（1，1），C（3，2）.

(1)、画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁的坐标：A₁（，）；

(2)、求△ABC的面积；

(3)、在y轴上找一点P（保留作图痕迹），使PA+PB的值最小，请直接写出点P的坐标：P（，）.

查看试题解析
21. 如图，△ABC为等腰直角三角形，∠ACB＝90°，E是AC上一点，D是BC延长线上一点，连结AD.

(1)、若AD＝BE.求证：∠CBE＝∠CAD.

(2)、若BC＝2，△ABD是等腰三角形，求CD的长.

查看试题解析
22. 随着新冠疫情的出现，口罩成为日常生活的必需品，某医药公司每月生产甲、乙两种型号的防疫口罩共20万只，且所有口罩当月全部卖出，其中成本、售价如表：

甲

乙

成本

12元/只

4元/只

售价

18元/只

6元/只

(1)、若该公司三月份的利润为100万元，求生产甲、乙两种型号的防疫口罩分别是多少万只？（利润＝售价-成本）

(2)、如果该公司四月份投入成本不超过216万元，该医药公司四月份最多只能生产甲种防疫口罩多少万只？

(3)、某学校到该公司购买乙型口罩有如下两种方案，方案一：乙型口罩一律打9折：方案二：购买168元会员卡后，乙型口罩一律8折，请帮学校设计出合适的购买方案.

查看试题解析
23. 已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点B，将△ADE沿DE折叠，点A对应点为F点.

(1)、如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；

(2)、如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小：

(3)、如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB＝9，求BG的长.

查看试题解析

	甲	乙
成本	12元/只	4元/只
售价	18元/只	6元/只